
已知a+b=﹣4,ab=2,则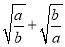 的值等于 .
的值等于 .
科目:初中数学 来源:人教版八年级下册数学 第16章 二次根式 单元检测卷 题型:单选题
化简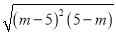 的正确结果是( )
的正确结果是( )
A. (m﹣5) 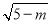 B. (5﹣m)
B. (5﹣m) 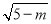 C. m﹣5
C. m﹣5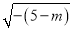 D. 5﹣m
D. 5﹣m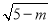
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区公益中学2017-2018学年八年级上学期期中数学 题型:单选题
长度分别为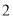 ,
, 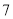 ,
, 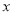 的三条线段能组成一个三角形,
的三条线段能组成一个三角形, 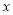 的值可以是( )
的值可以是( )
A. 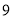 B.
B. 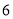 C.
C. 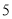 D.
D. 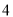
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学第三章圆单元检测卷 题型:单选题
如图,PA、PB是⊙O的切线,切点分别是A,B,如果∠P=60°,那么∠AOB等于( )
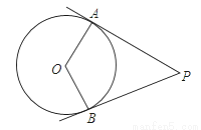
A. 60° B. 90° C. 120° D. 150°
C 【解析】试题分析:∵PA是圆的切线. ∴∠OAP=90° 同理∠OBP=90° 根据四边形内角和定理可得:∠AOB=360°-∠OAP-∠OBP-∠P=360°-90°-90°-60°=120° 故选C.查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学第三章圆单元检测卷 题型:单选题
如图,△ABC是⊙O的内接三角形,若∠C=60°,则∠AOB的度数是( )
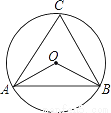
A. 30° B. 60° C. 90° D. 120°
D 【解析】∵∠AOB和∠C是同弧所对的圆心角和圆周角, ∴∠AOB=2∠C=120°, 故选D.查看答案和解析>>
科目:初中数学 来源:人教版八年级下册数学全册综合测试卷 题型:填空题
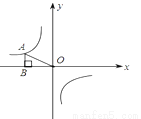
如图,双曲线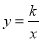 (
(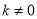 )上有一点A,过点A作AB⊥x轴于点B,△AOB的面积为2,则该双曲线的表达式为 ________ .
)上有一点A,过点A作AB⊥x轴于点B,△AOB的面积为2,则该双曲线的表达式为 ________ .
查看答案和解析>>
科目:初中数学 来源:人教版八年级下册数学全册综合测试卷 题型:单选题
若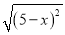 =x﹣5,则x的取值范围是( )
=x﹣5,则x的取值范围是( )
A. x<5 B. x≤5 C. x≥5 D. x>5
C 【解析】分析:本题考查的是 的运用. 解析:∵=x﹣5,∴ 故选C.查看答案和解析>>
科目:初中数学 来源:人教版 2018年春 七年级数学下册 第五章 相交线与平行线 几何证明题 题型:解答题
如图,∠BAP+∠APD=180°,∠1=∠2. 求证:∠E=∠F
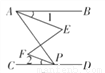
查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学全册综合测试卷 题型:解答题
如图,在△ABC中,CA=CB,点D在BC上,且AB=AD=DC,求∠C的度数.
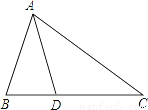
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com