
 如图,AB∥CD,NB、ND分别平分∠ABM和∠MDC,求证:∠M=2∠N.
如图,AB∥CD,NB、ND分别平分∠ABM和∠MDC,求证:∠M=2∠N. 分析 过点M作直线ME∥AB,过点N作直线NF∥AB,由平行线的性质可得∠BMD=∠ABM+∠CDM,∠BND=∠ABN+∠CDN,再根据角平分线的性质,即可得到结论.
解答  证明:过点M作直线ME∥AB,过点N作直线NF∥AB,
证明:过点M作直线ME∥AB,过点N作直线NF∥AB,
又∵AB∥CD,
∴ME∥CD,NF∥CD(平行于同一直线的两直线互相平行),
∴∠ABM=∠BME,∠CDM=∠DME(两直线平行,内错角相等),
∴∠BMD=∠BME+∠DME=∠ABM+∠CDM.
同理可得:∠BND=∠ABN+∠CDN.
∵BN,DN分别平分∠ABM,∠MDC,
∴∠ABM=2∠ABN,∠CDM=2∠CDN(角平分线定义)
∴∠BMD=2∠BND.
点评 本题考查了平行线的性质,正确作出辅助线是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
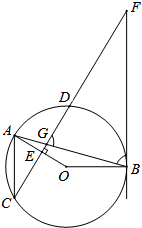 如图,在⊙O中,弦AB与弦CD相交于点G,OA⊥CD于点E,过点B的直线与CD的延长线交于点F,AC∥BF.
如图,在⊙O中,弦AB与弦CD相交于点G,OA⊥CD于点E,过点B的直线与CD的延长线交于点F,AC∥BF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
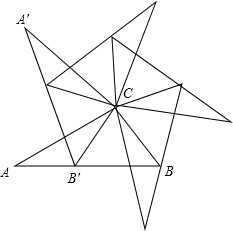 如图,在△ABC中,以点C为旋转中心,将△ABC旋转到△A′B′C的位置,其中A′,B′分别是A,B的对应点,且点B′在AB边上,按照上述方法旋转△A′B′C,…,这样共旋转四次恰好构成一个旋转对称图形.
如图,在△ABC中,以点C为旋转中心,将△ABC旋转到△A′B′C的位置,其中A′,B′分别是A,B的对应点,且点B′在AB边上,按照上述方法旋转△A′B′C,…,这样共旋转四次恰好构成一个旋转对称图形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,A、B之间是一座山,一条铁路要通过A、B两地,在A地测得铁路走向是北偏东65°18′,如果A、B两地同时开工,那么在B地按北偏西多少度施工,才有使铁路在山腹中准确接通?为什么?
如图,A、B之间是一座山,一条铁路要通过A、B两地,在A地测得铁路走向是北偏东65°18′,如果A、B两地同时开工,那么在B地按北偏西多少度施工,才有使铁路在山腹中准确接通?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com