
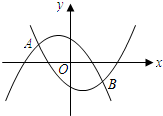
如图所示,两条直线分别表示函数y1=kx和y2=mx+n,请根据图象,回答下列问题:

(1)直线AB表示________的图象,直线OB表示________的图象.
(2)函数y1=kx随x的增大而________,函数y2=mx+n随x的减小而________.
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
| 1 | 2 |
 ,l2之间,且l与两条抛物线分别交于C,D两点,求线段CD的最大值?
,l2之间,且l与两条抛物线分别交于C,D两点,求线段CD的最大值?查看答案和解析>>
科目:初中数学 来源:新教材完全解读 七年级数学 (下册) (配人教版新课标) (第1次修订版) 配人教版新课标 题型:044
(1)一条直线可以把平面分成两部分,如图所示,两条直线可以把平面分面几个部分?三条直线可以把平面分成几个部分?试画图说明.
(2)四条直线最多可以把平面分成几个部分?试画出示意图,并说明这四条直线的位置关系.
(3)平面上有n条直线,每两条直线都恰好相交,且没有三条直线交于点一点,处于这种位置的n条直线分一个平面所成的区域最多,记为an,试写出an与n之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 时,设y1=-ax2-ax+1与x轴分别交于M,N两点(M在N的左边),y2=ax2-ax-1与x轴分别交于E,F两点(E在F的左边),观察M,N,E,F四点坐标,请写出一个你所得到的正确结论,并说明理由;
时,设y1=-ax2-ax+1与x轴分别交于M,N两点(M在N的左边),y2=ax2-ax-1与x轴分别交于E,F两点(E在F的左边),观察M,N,E,F四点坐标,请写出一个你所得到的正确结论,并说明理由;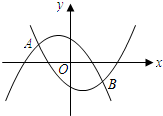 ,l2之间,且l与两条抛物线分别交于C,D两点,求线段CD的最大值?
,l2之间,且l与两条抛物线分别交于C,D两点,求线段CD的最大值?查看答案和解析>>
科目:初中数学 来源:2008年江西省中考数学试卷(解析版) 题型:解答题
 时,设y1=-ax2-ax+1与x轴分别交于M,N两点(M在N的左边),y2=ax2-ax-1与x轴分别交于E,F两点(E在F的左边),观察M,N,E,F四点坐标,请写出一个你所得到的正确结论,并说明理由;
时,设y1=-ax2-ax+1与x轴分别交于M,N两点(M在N的左边),y2=ax2-ax-1与x轴分别交于E,F两点(E在F的左边),观察M,N,E,F四点坐标,请写出一个你所得到的正确结论,并说明理由;
查看答案和解析>>
科目:初中数学 来源:吉林省期末题 题型:解答题
 (其中a为常数,且a>0)
(其中a为常数,且a>0)
 时,设
时,设 与x轴分别交于M、N两点(M在N的左边),y2=ax2-ax-1与x轴分别交于E、F两点(E在F的左边),观察M、N、E、F四点坐标,请写出一个你所得到的正确结论,并说明理由。
与x轴分别交于M、N两点(M在N的左边),y2=ax2-ax-1与x轴分别交于E、F两点(E在F的左边),观察M、N、E、F四点坐标,请写出一个你所得到的正确结论,并说明理由。  都垂直于x轴,
都垂直于x轴, 分别经过A、B两点,在直线
分别经过A、B两点,在直线 之间,且与两条抛物线分别交于C、D两点,求线段CD长的最大值。
之间,且与两条抛物线分别交于C、D两点,求线段CD长的最大值。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com