
若⊙A的半径为5,点A的坐标为(3,4),点P的坐标为(5,8),则点P的位置为( )
A. 在⊙A内 B. 在⊙A上 C. 在⊙A外 D. 不确定
A 【解析】∵A的坐标为(3,4),点P的坐标是(5,8), ∴AP= ∵⊙A的半径为5, ∴ . ∴点P在⊙A的内部. 故选A. 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:解答题
解分式方程:(1) 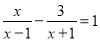
(2)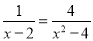 .
.
查看答案和解析>>
科目:初中数学 来源:北京市平谷区2018届初三第一学期期末数学试卷 题型:填空题
圆心角为120°,半径为6cm的扇形的弧长是_________________cm(结果不取近似值).
4π 【解析】弧长为: .查看答案和解析>>
科目:初中数学 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:解答题
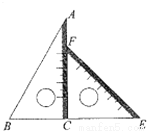
数学拓展课程《玩转学具》课堂中,小陆同学发现:一副三角板中,含45°的三角板的斜边与含30°的三角板的长直角边相等,于是,小陆同学提出一个问题:如图,将一副三角板直角顶点重合拼放在一起,点B,C,E在同一直线上,若BC=2,
求AF的长.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:单选题
如图,在△ABC,P为AB上一点,连结CP,下列条件中不能判定△ACP∽△ABC的是( )

A. ∠ACP=∠B B. ∠APC=∠ACB C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:上海浦东新区2017-2018学年九年级上学期期末数学试卷(初三一模) 题型:解答题
已知抛物线y=ax2+bx+5与x轴交于点A(1,0)和点B(5,0),顶点为M.点C在x轴的负半轴上,且AC=AB,点D的坐标为(0,3),直线l经过点C、D.
(1)求抛物线的表达式;
(2)点P是直线l在第三象限上的点,联结AP,且线段CP是线段CA、CB的比例中项,
求tan∠CPA的值;

(3)在(2)的条件下,联结AM、BM,在直线PM上是否存在点E,使得∠AEM=∠AMB.若存在,求出点E的坐标;若不存在,请说明理由.
(1);(2) ;(3)E的坐标为(-2,-4)或(4,-4). 【解析】试题分析:(1)把A、B两点带入抛物线解析式,求得a、b的值,即可得到抛物线解析式; (2)由AC=AB且点C在点A的左侧,及线段CP是线段CA、CB的比例中项,可得CP=, 由两边对应成比例且夹角相等的三角形相似,可得△CPA∽△CBP,由此∠CPA= ∠CBP. 过P作PH⊥x轴于H,易得PH=4...查看答案和解析>>
科目:初中数学 来源:上海浦东新区2017-2018学年九年级上学期期末数学试卷(初三一模) 题型:填空题
已知点(-1,m)、(2,n)在二次函数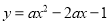 的图像上,如果m>n,那么a 0(用“>”或“<”连接).
的图像上,如果m>n,那么a 0(用“>”或“<”连接).
查看答案和解析>>
科目:初中数学 来源:云南省2018届九年级上学期期中考试数学试卷 题型:解答题
如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
(1)求二次函数的解析式;
(2)求点B、点C的坐标;
(3)该二次函数图象上有一动点D(x,y),使S△ABD=S△ABC,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省海口市九年级数学科期末检测题 题型:单选题
从1~10这十个数中随机取出一个数,取出的数是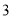 的倍数的概率是( )
的倍数的概率是( )
A. 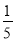 B.
B. 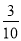 C.
C. 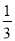 D.
D. 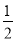
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com