练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．下列图形中，既是轴对称图形，又是中心对称图形的是（　　）
    A．B．C．D．

    分析 根据轴对称图形和中心对称图形对各选项分析判断即可得解．

    解答 解：A、不是轴对称图形，是中心对称图形，故本选项错误；
    B、是轴对称图形，不是中心对称图形，故本选项错误；
    C、既是轴对称图形，又是中心对称图形，故本选项正确；
    D、是轴对称图形，不是中心对称图形，故本选项错误．
    故选C．

    点评 本题考查了中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    17．已知点A（3，4），点B为直线x=-1上的动点，设B（-1，y）．
    （1）如图①，若∠AOB=90°，求y的值；
    （2）如图②，若有AO=AB，则y的值为±2$\sqrt{6}$
    （3）如图③，若在x轴上有一点C（x，0）且-1＜x＜3，BC⊥AC垂足为点C；若AB与y轴正半轴的所夹锐角为α，则tanα是否存在最大值？如果存在，直接写出这个最大值，如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

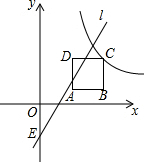    18．边长为a的正方形ABCD在平面直角坐标系中的位置如图所示，其中AB与x轴平行（点B在点A的右侧），点A的坐标为（2，1），反比例函数y=$\frac{m}{x}$经过点C，直线l：y=kx-2（k≠0）与y轴交于点E．
    （1）当a=2时，试完成下面的问题：
    ①求反比例函数的解析式；
    ②当直线l把正方形ABCD分为面积相等的两部分时，求k的值；
    （2）若k=2，当直线l与正方形ABCD的边CD能相交（设交点为F），且DF不超过3时，直接写出a的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．不等式组 $\left\{{\begin{array}{l}{\frac{x+1}{2}＜1}\\{2x-1≤3x}\end{array}}\right.$的整数解的个数是（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

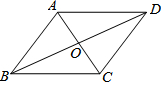    2．如图，平行四边形ABCD的对角线AC与BD相交于点O，要使它成为矩形，需再添加的条件是（　　）
    A．AO=OCB．AC=BDC．AC⊥BDD．BD平分∠ABC

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．如图，矩形ABCD中，AB=10，BC=8，P为AD的中点，将△ABP沿BP翻折至△EBP（点A落到点E处），连接DE，则图中与∠APB相等的角的个数为（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

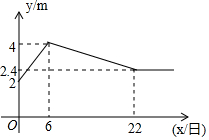    19．如图，是皖韵水库进入5月份以来的水位y米与x日的函数图象，为了避免过度捕捞，当水位低于3米时就不适宜渔船打捞作业，根据图象可知，5月份能打捞的天数有（　　）天．
    A．11B．12C．13D．14

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

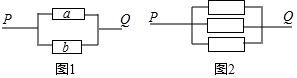    16．在物理实验中，当电流在一定时间段内正常通过电子元件时，每个电子元件的状态有两种可能；通电或断开，并且这种状态的可能性相等．
    （1）如图1，当有2个电子元件a、b并联时，请你用树状图表示图中P、Q之间电流能否通过的所有可能情况，并求出P、Q之间有电流通过的概率；
    （2）如图2，当有3个电子元件并联时，求P、Q之间有电流通过的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如图，在平面直角坐标系中，O是坐标原点，直线y=-$\frac{3}{4}$x+9与x轴，y轴分别交于B，C两点，抛物线y=-$\frac{1}{4}$x2+bx+c经过B，C两点，与x轴的另一个交点为点A，动点P从点A出发沿AB以每秒3个单位长度的速度向点B运动，运动时间为t（0＜t＜5）秒．
    （1）求抛物线的解析式及点A的坐标；
    （2）在点P从点A出发的同时，动点Q从点B出发沿BC以每秒3个单位长度的速度向点C运动，动点N从点C出发沿CA以每秒$\frac{3\sqrt{10}}{5}$个单位长度的速度向点A运动，运动时间和点P相同．
    ①记△BPQ的面积为S，当t为何值时，S最大，最大值是多少？
    ②是否存在△NCQ为直角三角形的情形？若存在，求出相应的t值；若不存在，请说明理由．

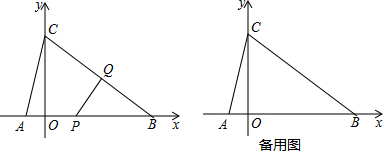
    查看答案和解析>>

    同步练习册答案