
阅读下列材料:
实验数据显示,一般成人喝250毫升低度白酒后,其血液中酒精含量(毫克/百毫升)随时间的增加逐步增高达到峰值,之后血液中酒精含量随时间的增加逐渐降低.
小带根据相关数据和学习函数的经验,对血液中酒精含量随时间变化的规律进行了探究,发现血液中酒精含量y是时间x的函数,其中y表示血液中酒精含量(毫克/百毫升),x表示饮酒后的时间(小时).
下表记录了6小时内11个时间点血液中酒精含量y(毫克/百毫升)随饮酒后的时间x(小时)(x>0)的变化情况.
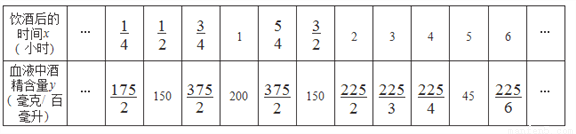
下面是小带的探究过程,请补充完整:
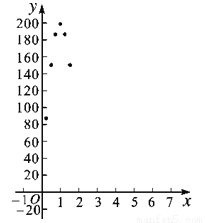
(1)如图,在平面直角坐标系xOy中,以上表中各对数值为坐标描点,图中已给出部分点,请你描出剩余的点,画出血液中酒精含量y随时间x变化的函数图象;
(2)观察表中数据及图象可发现此函数图象在直线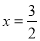 两侧可以用不同的函数表达式表示,请你任选其中一部分写出表达式;
两侧可以用不同的函数表达式表示,请你任选其中一部分写出表达式;
(3)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:30在家喝完250毫升低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
(1)答案见解析;(2)(0<x≤)或(x>);(3)不能. 【解析】试题分析:(1)利用描点法画出函数图象即可; (2)利用待定系数法即可解决问题; (3)把y=20代入反比例函数y=得x=11.25.喝完酒经过11.25小时为早上7:45,即早上7:45以后血液中的酒精含量小于或等于20毫克/百毫升.由此即可判断. 试题解析:(1)图象如图所示. (2)y=-20...科目:初中数学 来源:山东省淄博市2017-2018学年七年级上学期期中考试数学试卷 题型:填空题
下列各数:-3,-2.5,+2.25,0,+24%,+3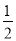 ,
, 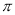 ,-
,- 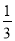 ,10,其中正有理数有________________________;负分数有_______________.
,10,其中正有理数有________________________;负分数有_______________.
查看答案和解析>>
科目:初中数学 来源:北京市顺义区2018届初三上学期期末考试数学试卷 题型:单选题
实数a,b,c,d在数轴上的对应点位置如图所示,这四个数中,绝对值最小的是

A. a B. b C. c D. d
C 【解析】根据数轴上某个数与原点的距离的大小求得结论. 【解析】 由图可知:c到原点O的距离最短, 所以在这四个数中,绝对值最小的是c. 故选C. “点睛”本题考查了绝对值的定义、实数大小比较问题,熟练掌握绝对值最小的数就是到原点距离最小的数.查看答案和解析>>
科目:初中数学 来源:2017-2018学年陕西安市九年级(上)期末数学试卷 题型:单选题
二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:
①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>﹣1时,y的值随x值的增大而增大.
其中正确的结论有( )
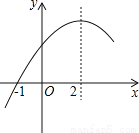
A.1个 B.2个 C.3个 D.4个
B 【解析】 试题分析:根据抛物线的对称轴为直线x=﹣=2,则有4a+b=0;观察函数图象得到当x=﹣3时,函数值小于0,则9a﹣3b+c<0,即9a+c<3b;由于x=﹣1时,y=0,则a﹣b+c=0,易得c=﹣5a,所以8a+7b+2c=8a﹣28a﹣10a=﹣30a,再根据抛物线开口向下得a<0,于是有8a+7b+2c>0;由于对称轴为直线x=2,根据二次函数的性质得到当x>2时...查看答案和解析>>
科目:初中数学 来源:2017-2018学年陕西安市九年级(上)期末数学试卷 题型:单选题
已知一元二次方程ax2+bx+c=0(a≠0)中,下列说法:
①若a+b+c=0,则b2﹣4ac>0;
②若方程两根为﹣1和2,则2a+c=0;
③若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
④若b=2a+c,则方程有两个不相等的实根.其中正确的有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
C 【解析】试题解析:①当时,有若 即方程有实数根了, 故错误; ②把 代入方程得到:(1) 把代入方程得到: (2) 把(2)式减去(1)式×2得到: 即: 故正确; ③方程 有两个不相等的实数根, 则它的 而方程的 ∴必有两个不相等的实数根.故正确; ④若则 故正确. ②③④都正确, 故选C.查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期八年级数学期中试卷 题型:解答题
某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.该商场两次共购进这种运动服多少套?
该商场两次共购进这种运动服600套. 【解析】试题分析:设第一次购进x套,则第二次购进2x套,第一批购进数量为,第二批购进数量为,根据题意列出方程+10=,解出x并验证是否为增根. 试题解析: 【解析】 设第一次购进x套,则第二次购进2x套, ,解得 x=200, 经检验x=200是方程的解. 200+200×2=600. 答:该商场两次共购进这种运动服...查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期八年级数学期中试卷 题型:填空题
已知关于x的分式方程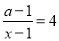 的解为非负数,则a的取值范围是_____________.
的解为非负数,则a的取值范围是_____________.
查看答案和解析>>
科目:初中数学 来源:北京市分校2017-2018学年度第一学期期中初二数学试卷 题型:解答题
阅读下列材料
通过小学的学习我们知道,分数可分为“真分数”和“假分数”.而假分数都可化为带分数,如: 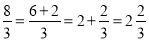 .
.
我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.
如: 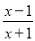 ,
, 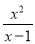 这样的分式就是假分式;再如:
这样的分式就是假分式;再如: 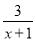 ,
, 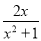 这样的分式就是真分式.
这样的分式就是真分式.
类似的,假分式也可以化为带分式(即:整式与真分式的和的形式).
如: 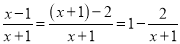 ;
; 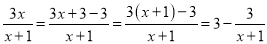 ;
;
再如: 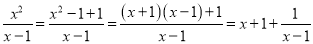 .
.
解决下列问题:
(1)分式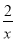 是 分式(填“真分式”或“假分式”);
是 分式(填“真分式”或“假分式”);
(2)假分式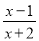 可化为带分式 的形式;
可化为带分式 的形式;
(3)如果分式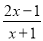 的值为整数,那么x的整数值为 .
的值为整数,那么x的整数值为 .
查看答案和解析>>
科目:初中数学 来源:福建省2016-2017学年八年级下学期期末考试数学试卷 题型:单选题
如图,在菱形ABCD中,AB的垂直平分线EF交对角线AC于点F,垂足为点E,连接DF,且∠CDF=24°, 则∠DAB等于( )
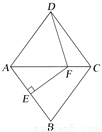
A. 102° B. 104° C. 106° D. 114°
B 【解析】【解析】 如图,连接BD,BF,∵四边形ABCD是菱形,∴AD=CD,∴∠DAC=∠DCA.∵EF垂直平分AB,AC垂直平分BD,∴AF=BF,BF=DF,∴AF=DF,∴∠FAD=∠FDA,∴∠DAC+∠FDA+∠DCA+∠CDF=180°,即3∠DAC+∠CDF=180°.∵∠CDF=24°,∴3∠DAC+24°=180°,则∠DAC=52°,∴∠DAB=2∠DAC=104...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com