
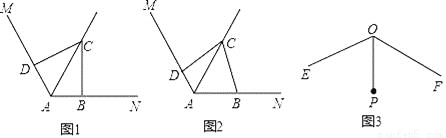
已知∠MAN=120°,点C是∠MAN的平分线AQ上的一个定点,点B,D分别在AN,AM上,连接BD.
【发现】
(1)如图1,若∠ABC=∠ADC=90°,则∠BCD= °,△CBD是 三角形;
【探索】
(2)如图2,若∠ABC+∠ADC=180°,请判断△CBD的形状,并证明你的结论;
【应用】
(3)如图3,已知∠EOF=120°,OP平分∠EOF,且OP=1,若点G,H分别在射线OE,OF上,且△PGH为等边三角形,则满足上述条件的△PGH的个数一共有 .(只填序号)
①2个 ②3个 ③4个 ④4个以上
科目:初中数学 来源:山西省吕梁市孝义市2016-2017学年九年级(上)期末考试数学试卷 题型:解答题
为了响应国家“自主创业”的号召,某大学毕业生开办了一个装饰品商店,采购了一种今年刚上市的饰品进行了30天的试销,购进价格为20元/件,销售结束后,得知日销售量P(件)与销售时间x(天)之间的关系如图(1)所示,销售价格Q(元/件)与销售时间x(天)之间的关系如图(2)所示.
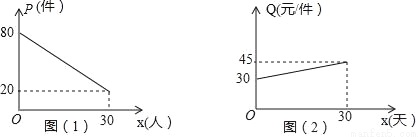
(1)根据图象直接写出:日销售量P(件)与销售时间x(天)之间的函数关系式为 ;销售单价
Q(元/件)与销售时间x(天)的函数关系式为 .(不要求写出自变量的取值范围)
(2)写出该商品的日销售利润W(元)和销售时间x(天)之间的函数关系式;(不要求写出自变量的取值范围)
(3)请问在30天的试销售中,哪一天的日销售利润最大?并求出这个最大利润.
(1)P=﹣2x+80,Q=x+30;(2)W=﹣x2+20x+800;(3)在30天的试销中,第10天的日销售利润最大,最大利润为900元 【解析】试题分析:(1)设P=kx+80,将(30,20)代入可求出k的值,得出日销售量P(件)与销售时间x(天)之间的函数关系式;设Q=mx+30,将(30,45)代入可求出m的值,得出Q(元/件)与销售时间x(天)的函数关系式; (2)根据销...查看答案和解析>>
科目:初中数学 来源:2017-2018学年黑龙江省大庆市杜尔伯特县九年级(上)期末数学试卷(五四学制) 题型:单选题
把抛物线y=﹣2x2向上平移1个单位,再向右平移1个单位,得到的抛物线是( )
A. y=﹣2(x+1)2+1 B. y=﹣2(x﹣1)2+1 C. y=﹣2(x﹣1)2﹣1 D. y=﹣2(x+1)2﹣1
B 【解析】试题解析:∵函数y=-2x2的顶点为(0,0), ∴向上平移1个单位,再向右平移1个单位的顶点为(1,1), ∴将函数y=-2x2的图象向上平移1个单位,再向右平移1个单位,得到抛物线的解析式为y=-2(x-1)2+1, 故选B.查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学北师大版上册:第4章 基本平面图形 单元测试卷 题型:填空题
如图,图中的线段共有________条,直线共有________条.
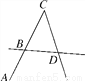
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学北师大版上册:第4章 基本平面图形 单元测试卷 题型:单选题
如图,一条流水生产线上L1、L2、L3、L4、L5处各有一名工人在工作,现要在流水生产线上设置一个零件供应站P,使五人到供应站P的距离总和最小,这个供应站设置的位置是( )
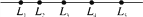
A. L2处 B. L3处 C. L4处 D. 生产线上任何地方都一样
B 【解析】试题分析:设在L3处为最佳,求出此时的总距离为L1L5+L2L4,假如设于任意的X处,求出总距离为L1L5+L2L4+L3X,和L1L5+L2L4比较即可. 【解析】 在5名工人的情况下,设在L3处为最佳,这时总距离为L1L5+L2L4, 理由是:如果不设于L3处,而设于X处,则总距离应为L1L5+L2L4+L3X>L1L5+L2L4, 即在L3处5个工人到供...查看答案和解析>>
科目:初中数学 来源:山东省德州地区2017-2018学年度第一学期期末检测八年级数学试卷 题型:解答题
如图,在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数.
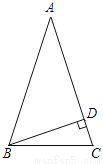
查看答案和解析>>
科目:初中数学 来源:山东省德州地区2017-2018学年度第一学期期末检测八年级数学试卷 题型:填空题
一个凸多边形的内角和与外角和相等,它是______边形.
四. 【解析】设这个正多边形的边数是n,则(n-2)•180°=360°,解得n=4.所以这个正多边形是四边形.查看答案和解析>>
科目:初中数学 来源:广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型:解答题
如图,某小区有一块长为18米,宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为60米2,两块绿地之间及周边留有宽度相等的人行通道.求人行通道的宽度.
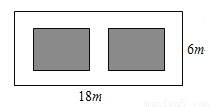
查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十八章达标检测卷 题型:单选题
正方形具有而菱形不具有的性质是
A.四条边相等 B.对角线互相垂直平分
C.对角线平分一组对角 D.对角线相等
D 【解析】 试题分析:正方形的性质四条边相等,四个角相等对角线相等且垂直,互相平分.菱形的性质四条边相等,对角线垂直且互相平分.所以选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com