已知,?ABCD的周长为52,自顶点D作DE⊥AB,DF⊥BC,垂足分别是E、F.若DE=5,DF=8,求?ABCD的两边AB、BC长和BE+BF的长.
解:对于平行四边形ABCD有两种情况:
(1)当∠A为锐角时,如图1,
设AB=a,BC=b,
∵平行四边形ABCD,DE⊥AB,DF⊥BC,
∴AB×DE=BC×DF,AB=CD,BC=DA,
又∵DE=5,DF=8,
∴5a=8b,
∵平行四边形ABCD的周长为52,
∴2(a+b)=52,
∴a+b=26,
解方程组
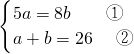
,
∴由②得:a=26-b ③,
∴把③代入①得:b=10,
∴a=16,
∵
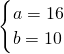
,
∴
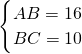
,
∴AB=CD=16,AD=BC=10,
∵DE=5,DF=8,
∴在Rt△ADE中,AE=5

,
∴BE=AB-AE=16-5

,
∴在Rt△DFC中,CF=8

,
∵F点在CB的延长线上,
∴BF=CF-BC=8

-10,
∴BE+BF=(16-5

)+(8

-10)=6+3

,
(2)当∠D为锐角时,如图2,
设AB=a,BC=b,
∵平行四边形ABCD,DE⊥AB,DF⊥BC,
∴AB×DE=BC×DF,AB=CD,BC=DA,
又∵DE=5,DF=8,
∴5a=8b,
∵平行四边形ABCD的周长为52,
∴2(a+b)=52,
∴a+b=26,
解方程组
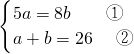
,
∴由②得:a=26-b ③,
∴把③代入①得:b=10,
∴a=16,
∵
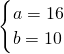
,
∴
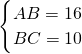
,
∴AB=CD=16,AD=BC=10,
∵DE=5,DF=8,
∴在Rt△ADE中,AE=5

,
∴在Rt△DFC中,CF=8

,
∴BE=BA+AE=16+5

,BF=BC+CF=10+8

,
∴BE+BF=(16+5

)+(10+8

)=26+13

.
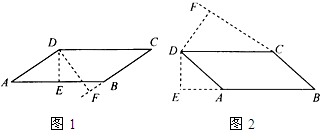
分析:根据∠A为锐角或∠D为锐角分情况进行讨论,(1)当∠A为锐角时,根据题意画出图形,做出辅助线,设AB=a,BC=b,根据平行四边形的面积公式推出AB×DE=BC×DF,即5a=8b,再根据平行四边形的性质推出AB=CD,BC=DA后,由周长公式即可推出2(a+b)=52,通过解方程组
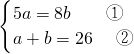
,推出
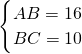
,即可求出AB=CD=16,AD=BC=10,然后根据勾股定理即可推出AE和CF的长度,根据图形即可求出BE=AB-AE=16-5

,BF=CF-BC=8

-10,通过计算即可求出BE+BF的长度,(2)当∠D为锐角时,根据题意画出图形,根据(1)中所求出的AE=5

,CF=8

,根据图形即可推出BE=BA+AE=16+5

,BF=BC+CF=10+8

,即可求出BE+BF=(16+5

)+(10+8

)=26+13

.
点评:本题主要考查平行四边形的性质,勾股定理,合并同类二次根式等知识点,关键在于根据∠A为锐角或∠D为锐角分情况进行讨论,根据平行四边形的面积公式和周长定理正确的列出方程组,并认真的求解,推出AB和BC的长度,熟练运用数形结合的思想进行求解.

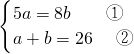 ,
,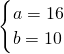 ,
,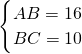 ,
, ,
, ,
, ,
, -10,
-10, )+(8
)+(8 -10)=6+3
-10)=6+3 ,
,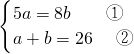 ,
,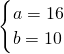 ,
,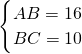 ,
, ,
, ,
, ,BF=BC+CF=10+8
,BF=BC+CF=10+8 ,
, )+(10+8
)+(10+8 )=26+13
)=26+13 .
.
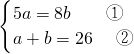 ,推出
,推出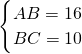 ,即可求出AB=CD=16,AD=BC=10,然后根据勾股定理即可推出AE和CF的长度,根据图形即可求出BE=AB-AE=16-5
,即可求出AB=CD=16,AD=BC=10,然后根据勾股定理即可推出AE和CF的长度,根据图形即可求出BE=AB-AE=16-5 ,BF=CF-BC=8
,BF=CF-BC=8 -10,通过计算即可求出BE+BF的长度,(2)当∠D为锐角时,根据题意画出图形,根据(1)中所求出的AE=5
-10,通过计算即可求出BE+BF的长度,(2)当∠D为锐角时,根据题意画出图形,根据(1)中所求出的AE=5 ,CF=8
,CF=8 ,根据图形即可推出BE=BA+AE=16+5
,根据图形即可推出BE=BA+AE=16+5 ,BF=BC+CF=10+8
,BF=BC+CF=10+8 ,即可求出BE+BF=(16+5
,即可求出BE+BF=(16+5 )+(10+8
)+(10+8 )=26+13
)=26+13 .
.
