
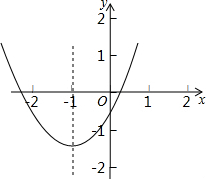 已知抛物线y=ax2+bx+c(a>0)的对称轴为直线x=-1,该抛物线与x轴的一个交点为(x1,0),且0<x1<1,有下列结论:①abc>0;②9a-3b+c>0;③b<a;④3a+c>0.其中正确结论的个数是( )
已知抛物线y=ax2+bx+c(a>0)的对称轴为直线x=-1,该抛物线与x轴的一个交点为(x1,0),且0<x1<1,有下列结论:①abc>0;②9a-3b+c>0;③b<a;④3a+c>0.其中正确结论的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①根据函数图象可得a、b、c的符号从而可以判断①是否正确;②由对称轴为直线x=-1,可知点(1,a+b+c),(-3,9a-3b+c)是抛物线是两个对称点,根据0<x1<1,a>0,判断点(1,a+b+c),所在的象限,可知点(-3,9a-3b+c)所在的象限,从而判断9a-3b+c的符号;
③由对称轴公式可知,-$\frac{b}{a}$=-1,即b=2a>0,而0<x1<1,抛物线开口向上,可知抛物线与y轴交于负半轴,c<0,可判断b、c的大小关系;
④由②③可知,把b=2a代入a+b+c>0得3a+c>0.
解答 解:①∵由函数图象开口向上可得a>0;顶点在y轴左侧可得a、b符号相同,故b>0;函数图象与y轴交于负半轴,可知c<0.
∴abc<0,故①错误;
②∵0<x1<1,
∴点(1,a+b+c)在第一象限,
又∵对称轴为直线x=-1,
∴(-3,9a-3b+c)在第二象限,故9a-3b+c>0,故②正确;
③∵-$\frac{b}{2a}$=-1,∴b=2a,
∴b-a=2a-a=a>0,
又0<x1<1,抛物线开口向上,
∴抛物线与y轴交于负半轴,c<0,
∴b>a>c,故③错误;
④把b=2a代入a+b+c>0得3a+c>0,故④正确;
故选B.
点评 本题考查二次函数图象与系数之间的关系,解题的关键是可以看懂二次函数的图象,根据图象可以判断a、b、c的符号,灵活变化,能够找出所求各结论需要的条件.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:解答题
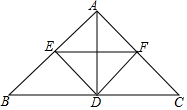 如图,在△ABC中,AB=AC,D是边BC上的一点,DE⊥AB,DF⊥AC,垂足分别是E、F,EF∥BC.
如图,在△ABC中,AB=AC,D是边BC上的一点,DE⊥AB,DF⊥AC,垂足分别是E、F,EF∥BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
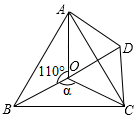 如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕着点C按顺时针方向旋转60°得到△ADC,连结OD,当α=150°时,△AOD是直角三角形.
如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕着点C按顺时针方向旋转60°得到△ADC,连结OD,当α=150°时,△AOD是直角三角形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将△ABE向右平移2cm得到△DCF.如果△ABE的周长是16cm,那么四边形ABFD的周长是( )
如图,将△ABE向右平移2cm得到△DCF.如果△ABE的周长是16cm,那么四边形ABFD的周长是( )| A. | 16 cm | B. | 18 cm | C. | 20 cm | D. | 21 cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知,甲地到乙地的路程为260千米,一辆大货车从甲地前往乙地运送物资,行驶2小时在途中某地出现故障,立即通知技术人员乘小汽车从甲地赶来维修(通知时间忽略不计),小汽车到达该地后经过20分钟修好大货车后以原速原路返回甲地,同时大货车以原来1.5倍的速度前往乙地,如图是两车距甲地的路程y(千米)与大货车所用时间x(小时)之间的函数图象,则大货车到达乙地比小汽车返回甲地晚2$\frac{1}{6}$小时.
已知,甲地到乙地的路程为260千米,一辆大货车从甲地前往乙地运送物资,行驶2小时在途中某地出现故障,立即通知技术人员乘小汽车从甲地赶来维修(通知时间忽略不计),小汽车到达该地后经过20分钟修好大货车后以原速原路返回甲地,同时大货车以原来1.5倍的速度前往乙地,如图是两车距甲地的路程y(千米)与大货车所用时间x(小时)之间的函数图象,则大货车到达乙地比小汽车返回甲地晚2$\frac{1}{6}$小时.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
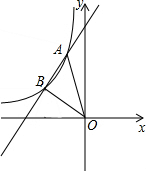 一次函数y=x+5的图象与反比例函数y=$\frac{k}{x}$(k<0)在第二象限的图象交于A(-1,n)和B两点.
一次函数y=x+5的图象与反比例函数y=$\frac{k}{x}$(k<0)在第二象限的图象交于A(-1,n)和B两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com