
已知一次函数y=kx+7的图像经过点A(2,3).
(1)求k的值;
(2)判断点B(-1,8),C(3,1)是否在这个函数的图像上,并说明理由;
(3)当-3<x<-1时,求y的取值范围.
【答案】(1)k=-2(2)点B不在,点C在,(3)9<y<13
【解析】
试题分析:(1)把点A(2,3)代入y=kx+7即可求出k的值;(2)点B(-1,8),C(3,1)的横坐标代入函数解析式验证即可;(3)根据x的取值范围,即可求出y的取值范围.
试题解析:(1)把点A(2,3)代入y=kx+7得:k=-2
(2)当x=-1时,y=-2×(-1)+7=9
∵9≠8∴点B不在抛物线上.
当x=3时,y=-2×3+7=1
∴点C在抛物线上
(3)当x=-3时,y=13,当x=-,1时,y=9,所以9<y<13
考点:一次函数.
【题型】解答题
【结束】
24
顺丰快递公司派甲、乙两车从A地将一批物品匀速运往B地,甲出发0.5h后乙开始出发,结果比甲早1(h)到达B地,如图,线段OP、MN分别表示甲、乙两车离A地的距离S(km)与时间t(h)的关系,a表示A、B两地之间的距离.请结合图中的信息解决如下问题:
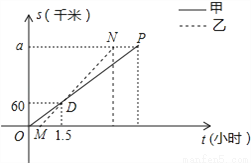
(1)分别计算甲、乙两车的速度及a的值;
(2)乙车到达B地后以原速立即返回,请问甲车到达B地后以多大的速度立即匀速返回,才能与乙车同时回到A地?并在图中画出甲、乙两车在返回过程中离A地的距离S(km)与时间t(h)的函数图象.
(1)甲、乙两车的速度分别为40km/h、60km/h,a的值是180km;(2)甲返回时的速度为90km/h 【解析】试题分析:(1)观察t轴,s轴表示的意义,利用v=求速度.(2) ,利用v=为等量列方程求解. 试题解析: (1)由图象得:甲的速度为:60÷1.5=40(km/h), 乙的速度为:60÷(1.5﹣0.5)=60(km/h), 求a的方法如下: ...科目:初中数学 来源:2017年广西防城港市中考数学模拟试卷 题型:填空题
将一些半径相同的小圆按如图所示的规律摆放,请仔细观察,第n个图形有 _________个小圆(用含n的代数式表示)

查看答案和解析>>
科目:初中数学 来源:江苏省徐州市区联校2017-2018学年七年级上学期期中联考数学试卷 题型:单选题
如图,检测4个足球,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数,从轻重的角度看,最接近标准的是
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:山东省诸城市2017-2018学年七年级上学期第二次月考数学试卷 题型:单选题
下列方程的变形中,正确的是( )
A. 方程 3x﹣2=2x+1,移项,得 3x﹣2x=﹣1+2
B. 方程 3﹣x=2﹣5(x﹣1),去括号,得 3﹣x=2﹣5x﹣1
C. 方程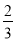 x=
x=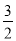 ,未知数系数化为 1,得 x=1
,未知数系数化为 1,得 x=1
D. 方程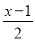 ﹣
﹣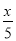 =1 化成 5(x﹣1)﹣2x=10
=1 化成 5(x﹣1)﹣2x=10
查看答案和解析>>
科目:初中数学 来源:山东省诸城市2017-2018学年七年级上学期第二次月考数学试卷 题型:单选题
如果3x2myn+1与﹣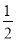 x2ym+3是同类项,则m,n的值为( )
x2ym+3是同类项,则m,n的值为( )
A. m=﹣1,n=3 B. m=1,n=3 C. m=﹣1,n=﹣3 D. m=1,n=﹣3
B 【解析】【解析】 ∵3x2myn+1与﹣x2ym+3是同类项,∴2m=2,n+1=m+3,解得m=1,n=3.故选B.查看答案和解析>>
科目:初中数学 来源:江苏省盐城市2017-2018学年八年级12月联合质量调研数学试卷 题型:解答题
求下列各式中的x的值:
(1)8x3+125=0;
(2)(x-3)2-9=0.
【答案】(1)x=-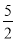 ;(2)x1=6或x2=0.
;(2)x1=6或x2=0.
【解析】试题分析:(1)立方根定义解方程.(2)平方根定义解方程.
试题解析:(1)8x3+125=0,
x3=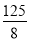 ,
,
x=-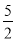 .
.
(2)(x-3)2-9=0,
(x-3)2=9,
x-3=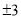 ,
,
x1=6或x2=0.
【题型】解答题
【结束】
19
(1)已知某数的平方根是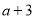 和
和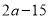 ,
, 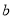 的立方根是
的立方根是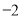 ,求
,求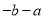 的平方根.
的平方根.
(2)已知y=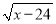 +
+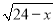 -8,求
-8,求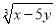 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市2017-2018学年八年级12月联合质量调研数学试卷 题型:填空题
在Rt△ABC中,∠C=90°,AC=3,BC=4,则点C到AB的距离是______.
【解析】∠C=90°,AC=3,BC=4,勾股定理知AB=5,设C到AB的距离是h,利用等面积法知,ACBC=hAB,所以h=. 故答案为查看答案和解析>>
科目:初中数学 来源:2016-2017学年陕西师大附中七年级(下)第一次月考数学试卷 题型:解答题
如图,完成下列推理过程.
已知:DE⊥AO于E,BO⊥AO,∠CFB=∠EDO.
证明:CF∥DO.
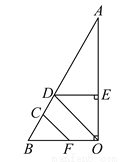
证明:∵DE⊥AO,BO⊥AO(已知)
∴∠DEA=∠BOA=90°(_________)
∴DE∥BO(________________________)
∴∠EDO=∠DOF(_______________________)
又∵∠CFB=∠EDO(__________)
∴∠DOF=∠CFB(____________)
∴CF∥DO(____________________)
垂直定义 同位角相等,两直线平行 两直线平行,内错角相等 已知 等量代换 同位角相等,两直线平行 【解析】由DE与BO都与AO垂直,利用垂直定义得到一对直角相等,利用同位角相等两直线平行得到DE与BO平行,利用两直线平行得到一对内错角相等,再由已知的一对角相等,等量代换得到一对同位角相等,利用同位角相等两直线平行即可得到CF与DO平行. 【解析】 ∵DE⊥AO,BO⊥AO(已知) ...查看答案和解析>>
科目:初中数学 来源:四川省遂宁市黄泥学校2016-2017学年上期八年级期中测评数学试卷 题型:单选题
下列多项式,能用公式法分解因式的有( )
①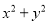 ②
②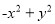 ③
③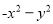 ④
④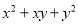
⑤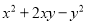 ⑥
⑥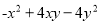
A. 2个 B. 3个 C. 4个 D. 5个
A 【解析】根据完全平方公式,平方差公式, 的特征可判定②可以利用平方差公式进行因式分解,⑥可以利用完全平方公式进行因式分解,因此本题正确选项是A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com