
已知:如图,点A,B,C,D在一条直线上,AB=CD,AE∥FD,且∠E=∠F.求证:EC=FB.

科目:初中数学 来源:广东省广州市越秀区2016-2017学年八年级下册数学期末考试试卷 题型:解答题
如图,正方形ABCD的对角线相交于点O,BC=6,延长BC至点E,使得CE=8,点F是DE的中点,连接CF、OF.
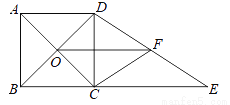
(1)求OF的长.
(2)求CF的长.
(1)7;(2)5. 【解析】试题分析:(1)由正方形的性质可知O为BD的中点,故此OF是△DBE的中位线,然后依据三角形中位线的性质解答即可; (2)在Rt△DCE中,利用勾股定理求出DE,再利用直角三角形斜边上中线等于斜边的一半求解即可. 试题解析:(1)∵四边形ABCD是正方形, ∴BC=CD=6,∠BCD=∠ECD=90°,OB=OD, ∵CE=8, ∴...查看答案和解析>>
科目:初中数学 来源:湖北省襄阳市襄城区2016-2017学年度上学期期末考试七年级数学试卷 题型:单选题
2016的相反数是:
A. 2016 B. -2016 C. 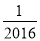 D. -
D. - 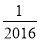
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(北师大版):期中检测题 题型:单选题
如图,已知MN是△ABC的边AB的垂直平分线,垂足为点F,∠CAB的平分线AD交BC于点D,且MN与AD交于点O,连接BO并延长交AC于点E,则下列结论中不一定成立的是( )
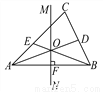
A. ∠CAD=∠BAD B. OE=OF C. AF=BF D. OA=OB
B 【解析】∵AD是∠CAB的平分线, ∴∠CAD=∠BAD,∴A正确; ∵BE不一定垂直AC, ∴无法判断OE、OF是否相等, ∴B错误; ∵MN是边AB的垂直平分线, ∴AF=BF,OA=OB, ∴C、D正确. 故选B.查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(北师大版):期中检测题 题型:单选题
若△ABC中,∠A∶∠B∶∠C=1∶2∶3,则△ABC一定是( )
A. 锐角三角形 B. 钝角三角形 C. 直角三角形 D. 等腰三角形
C 【解析】【解析】 ∵△ABC中,∠A:∠B:∠C=1:2:3,∴设∠A=x°,∠B=2x°,∠C=3x°,∵∠A+∠B+∠C=180,∴x+2x+3x=180°,∴x=30,∴∠C=90°,∠A=30°,∠B=60°,即△ABC是直角三角形,故选C.查看答案和解析>>
科目:初中数学 来源:重庆市校2017-2018学年八年级上学期第二阶段考试数学试卷 题型:填空题
如图,已知△DAC,△EBC均是等边三角形,点A,C,B在同一条直线上,AE,BD分别与CD,CE交于点M,N,下列结论:①△ACE≌△DCB; ②CM=CN;③AC=DN ;④∠DAE=∠DBC.其中正确的结论有________________.
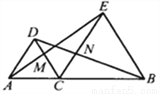
查看答案和解析>>
科目:初中数学 来源:重庆市校2017-2018学年八年级上学期第二阶段考试数学试卷 题型:单选题
如图所示,∠A+∠B+∠C+∠D+∠E的结果为( )
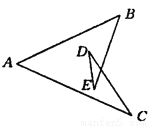
A. 90° B. 360° C. 180° D. 无法确定
C 【解析】如图,连接BC, ∵∠D+∠E+∠DOE=∠BOC+∠OCB+∠BOC=180°,∠DOE=∠BOC, ∴∠D+∠E=∠OBC+∠OCB, 又∵∠A+∠ABO+∠ACO+∠OBC+∠OCB=180°, ∴∠A+∠ABO+∠ACO+∠D+∠E=180°. 故选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(华师大版):期中检测题 题型:解答题
(1)计算:(2017-π)0-(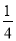 )-1+|-2|;
)-1+|-2|;
(2)化简:(1-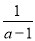 )÷(
)÷(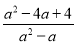 ).
).
查看答案和解析>>
科目:初中数学 来源:湖北省大冶市金湖街办2017-2018学年八年级上学期第二次月考(12月)数学试卷 题型:解答题
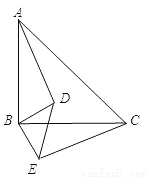
已知:如图,△ABC和△DBE均为等腰直角三角形.
(1)求证:AD=CE;
(2)猜想:AD和CE是否垂直?若垂直,请说明理由;若不垂直,则只要写出结论,不用写理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com