
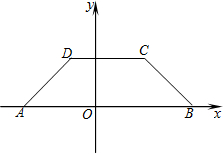
 已知等腰梯形ABCD中,A (-3,0),B (4,0),C (2,2),一条直线y=-
已知等腰梯形ABCD中,A (-3,0),B (4,0),C (2,2),一条直线y=- x+b将梯形ABCD面积等分,则b=________.
x+b将梯形ABCD面积等分,则b=________.
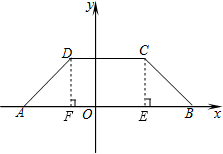 解:过点C作CE⊥AB于E,作DF⊥AB于F,
解:过点C作CE⊥AB于E,作DF⊥AB于F,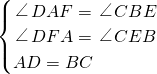 ,
, (AB+CD)×CE=
(AB+CD)×CE= ×(3+7)×2=10,
×(3+7)×2=10,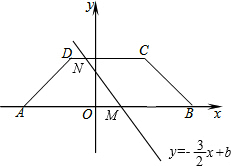
 x+b与梯形ABCD分别交于点M,N,
x+b与梯形ABCD分别交于点M,N, b,0),点N(
b,0),点N( (b-2),2),
(b-2),2),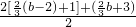 ,
,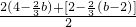 ,
,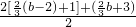 =
=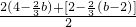 ,
, .
. .
.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com