
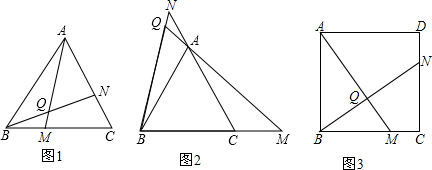
 在给出的如图,完成下列作图:
在给出的如图,完成下列作图:科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
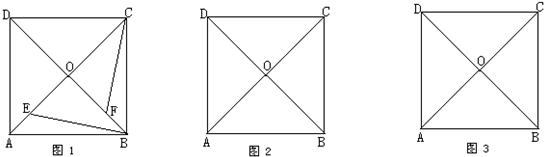
 =CN,AM、BN交于点Q,求证:∠BQM=60°.
=CN,AM、BN交于点Q,求证:∠BQM=60°.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:查看答案和解析>>
科目:初中数学 来源: 题型:044
某同学进行社会调查,随机抽查了某个地区的20个家庭的收入情况,并绘制了统计图(如图所示).请你根据统计图给出的信息回答:

(1)填写完成下表:

这20个家庭的年平均收入为______万元;
(2)样本中的中位数是______万元,众数是______万元;
(3)在平均数、中位数两数中,______更能反映这个地区家庭的年收入水平.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com