
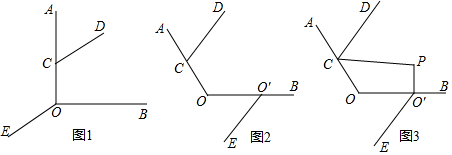
分析 (1)先根据平行线的性质得到∠AOE的度数,再根据直角、周角的定义即可求得∠BOE的度数;
(2)如图2,过O点作OF∥CD,根据平行线的判定和性质可得∠OCD、∠BO′E的数量关系;
(3)根据四边形内角和为360°,再根据(2)的结论,以及角平分线的定义即可求解.
解答 解:(1)∵CD∥OE,
∴∠AOE=∠OCD=120°,
∴∠BOE=360°-90°-120°=150°; (2)如图2,过O点作OF∥CD,
(2)如图2,过O点作OF∥CD,
∵CD∥OE,
∴OF∥OE,
∴∠AOF=180°-∠OCD,∠BOF=∠EO′O=180°-∠BO′E,
∴∠AOB=∠AOF+∠BOF=180°-∠OCD+180°-∠BO′E=360°-(∠OCD+∠BO′E)=120°,
∴∠OCD+∠BO′E=240°;
(3)∵CP是∠OCD的平分线,
∴∠OCP=$\frac{1}{2}$∠OCD,
∴∠CPO′=360°-90°-120°-∠OCP
=150°-$\frac{1}{2}$∠OCD
=150°-$\frac{1}{2}$(240°-∠BO′E)
=30°+$\frac{1}{2}$α.
点评 此题考查了平行线的判定和性质,直角、周角的定义,角平分线的定义,关键是得到∠OCD、∠BO′E的数量关系.


科目:初中数学 来源: 题型:解答题
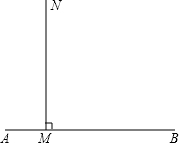 已知如图:射线MN⊥AB于点M,点C从M出发,以1cm/s的速度沿射线MN运动,AM=1,MB=4,设运动时间为ts,①当△ABC为等腰三角形时,求t的值;②当△ABC为直角三角形时,求t的值;③点C在运动的过程中,若△ABC为钝角三角形,则t的取值范围是0<t<2;若△ABC为锐角三角形,则t的取值范围是t>2.
已知如图:射线MN⊥AB于点M,点C从M出发,以1cm/s的速度沿射线MN运动,AM=1,MB=4,设运动时间为ts,①当△ABC为等腰三角形时,求t的值;②当△ABC为直角三角形时,求t的值;③点C在运动的过程中,若△ABC为钝角三角形,则t的取值范围是0<t<2;若△ABC为锐角三角形,则t的取值范围是t>2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,直线y=2x+2$\sqrt{3}$与x、y轴分别交于A、B两点,以OB为边在y轴左侧作等边△OBC,将△OBC沿y轴上下平移,使点C的对应点C′恰好落在直线AB上,则点C'的坐标为(-3,-6+2$\sqrt{3}$).
如图,直线y=2x+2$\sqrt{3}$与x、y轴分别交于A、B两点,以OB为边在y轴左侧作等边△OBC,将△OBC沿y轴上下平移,使点C的对应点C′恰好落在直线AB上,则点C'的坐标为(-3,-6+2$\sqrt{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
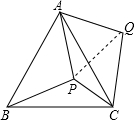 P是等边△ABC内部一点,∠APB、∠BPC、∠CPA的大小之比是5:6:7,将△ABP逆时针旋转,使得AB与AC重合,则以PA、PB、PC的长为边的三角形的三个角∠PCQ:∠QPC:∠PQC=3:4:2.
P是等边△ABC内部一点,∠APB、∠BPC、∠CPA的大小之比是5:6:7,将△ABP逆时针旋转,使得AB与AC重合,则以PA、PB、PC的长为边的三角形的三个角∠PCQ:∠QPC:∠PQC=3:4:2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4小时 | B. | 4.5小时 | C. | 5小时 | D. | 4小时或5小时 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com