
 如图,在平面直角坐标系xOy中,以点O为圆心的圆分别交x轴的正半轴于点M,交y轴的正半轴于点N.劣弧$\widehat{MN}$的长为$\frac{6}{5}$π,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A、B.
如图,在平面直角坐标系xOy中,以点O为圆心的圆分别交x轴的正半轴于点M,交y轴的正半轴于点N.劣弧$\widehat{MN}$的长为$\frac{6}{5}$π,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A、B.分析 (1)作OD⊥AB于D,由弧长公式和已知条件求出半径OM=$\frac{12}{5}$,由直线解析式求出点A和B的坐标,得出OA=3,OB=4,由勾股定理求出AB=5,再由△AOB面积的计算方法求出OD,即可得出结论;
(2)阴影部分的面积=△AOB的面积-扇形OMN的面积,即可得出结果.
解答 (1)证明:作OD⊥AB于D,如图所示: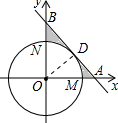
∵劣弧$\widehat{MN}$的长为$\frac{6}{5}$π,
∴$\frac{90π×OM}{180}$=$\frac{6}{5}π$,
解得:OM=$\frac{12}{5}$,
即⊙O的半径为$\frac{12}{5}$,
∵直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A、B,
当y=0时,x=3;当x=0时,y=4,
∴A(3,0),B(0,4),
∴OA=3,OB=4,
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵△AOB的面积=$\frac{1}{2}$AB•OD=$\frac{1}{2}$OA•OB,
∴OD=$\frac{OA×OB}{AB}$=$\frac{12}{5}$=半径OM,
∴直线AB与⊙O相切;
(2)解:图中所示的阴影部分的面积=△AOB的面积-扇形OMN的面积=$\frac{1}{2}$×3×4-$\frac{1}{4}$π×($\frac{12}{5}$)2=6-$\frac{36}{25}$π.
点评 本题考查了切线的判定、弧长公式、一次函数图象上点的坐标特征、勾股定理、扇形面积的计算等知识;熟练掌握切线的判定,由三角形的面积求出半径是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
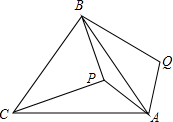 如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,连接BQ.若PA=6,PB=8,PC=10,则四边形APBQ的面积为24+9$\sqrt{3}$.
如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,连接BQ.若PA=6,PB=8,PC=10,则四边形APBQ的面积为24+9$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
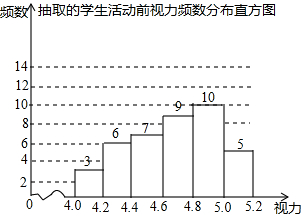 为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表所示.
为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表所示.| 分组 | 频数 |
| 4.0≤x<4.2 | 2 |
| 4.2≤x<4.4 | 3 |
| 4.4≤x<4.6 | 5 |
| 4.6≤x<4.8 | 8 |
| 4.8≤x<5.0 | 17 |
| 5.0≤x<5.2 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com