
 ,x1•x2=
,x1•x2= .再过P作PM⊥x轴于M,易证△APM∽△PBM,根据相似三角形对应边成比例得出PM2=BM×AM,即y02=(x2-x0)•(x0-x1),然后由点P是抛物线y=ax2+bx+c上的一点,将y0=ax02+bx0+c代入,整理后得出y0=-
.再过P作PM⊥x轴于M,易证△APM∽△PBM,根据相似三角形对应边成比例得出PM2=BM×AM,即y02=(x2-x0)•(x0-x1),然后由点P是抛物线y=ax2+bx+c上的一点,将y0=ax02+bx0+c代入,整理后得出y0=- ,x0=
,x0= ,即可判断.
,即可判断. 解:设抛物线y=ax2+bx+c与x轴的交点A(x1,0),B(x2,0),抛物线上一点P(x0,y0).
解:设抛物线y=ax2+bx+c与x轴的交点A(x1,0),B(x2,0),抛物线上一点P(x0,y0). ,x1•x2=
,x1•x2= .
. =
=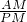 ,
, •x0+
•x0+ +y02=0,
+y02=0, •x0+
•x0+ +y02=0,
+y02=0, ,
, .
.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
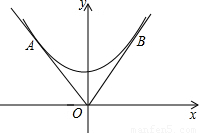
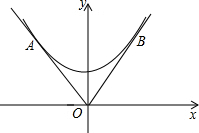 已知抛物线y=ax2+b(a>0,b>0),函数y=b|x|
已知抛物线y=ax2+b(a>0,b>0),函数y=b|x|查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(41):2.7 最大面积是多少(解析版) 题型:解答题
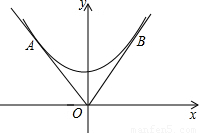
查看答案和解析>>
科目:初中数学 来源:第20章《二次函数和反比例函数》中考题集(41):20.5 二次函数的一些应用(解析版) 题型:解答题
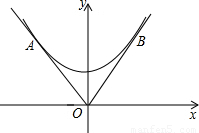
查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(42):2.4 二次函数的应用(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com