
如图所示是一个矩形被分成11个不同大小的正方形,其中最小正方形的边长是9 mm,求矩形的边长.

|
答:矩形的边长分别为177 mm、176 mm. 解:如图,给图中的小正方形编上号.①号正方形的边长是9 mm.设②号正方形的边长为x mm,则③号的边长为(x+9)mm;④号的边长为(x+9)+9=(x+18)mm;⑤号的边长为x+(x+9)=(2x+9)mm;⑥号的边长为x+(2x+9)=(3x+9)mm;⑦号的边长为(x+18)+9=(x+27)mm;⑧号的边长为(2x+9)+(3x+9)-(x+27)-(x+18)=(3x-27)mm;⑨号的边长为(3x-27)+(3x+9)=(6x-18)mm;⑩号的边长为(6x-18)+(3x-27)=(9x-45)mm; 注意到矩形的一边由⑩、⑨的正方形的边组成,长为(9x-45)+(6x-18)=(15x-63),又可由 故15x-63=(6x+81). 解上述方程得x=16,进而可得矩形的边长为15×16-63=177(mm)及(9x-45)+(2x+45)=11x=11×16=176(mm). |


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
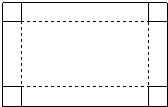 所示),可制成高是4cm,容积是512cm3的一个无盖长方体纸盒.
所示),可制成高是4cm,容积是512cm3的一个无盖长方体纸盒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 所示),可制成高是4cm,容积是512cm3的一个无盖长方体纸盒.
所示),可制成高是4cm,容积是512cm3的一个无盖长方体纸盒.查看答案和解析>>
科目:初中数学 来源:2013年辽宁省大连市五十八中中考数学模拟试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2010年辽宁省大连市中考数学二模试卷(解析版) 题型:解答题
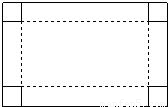
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com