练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    当x=2及x=﹣3时，分别求出下列函数的函数值：

    ①y=（x+1）（x﹣2）；

    ②y=．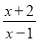

    ①0，10；②4， 【解析】试题分析：①把x=2和x=﹣3分别代入函数y=（x+1）（x﹣2）计算即可求解； ②把x=2及x=﹣3分别代入函数y=计算即可求解． 试题解析：①当x=2时，y=（x+1）（x﹣2）=（2+1）（2﹣2）=0， 当x=﹣3时，y=（x+1）（x﹣2）=（﹣3+1）（﹣3﹣2）=10； ②当x=2时，y==4． 当x=﹣3时，y==. ...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省扬州市2017-2018学年八年级上学期期末考试数学试卷 题型：填空题

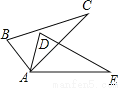
    如图，△ABC≌△ADE，若∠B=80°，∠C=30°，则∠EAD的度数为________．

    70° 【解析】试题解析：∵△ABC≌△ADE，∠B=80°，∠C=30°， ∴∠B=∠D=80°，∠E=∠C=30°， ∴∠EAD=180°-∠D-∠E=70°， 故答案为：70°.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018 北师大版七年级数学下册 第三章　变量之间的关系 单元测试卷 题型：填空题

    李老师带领x名学生到某动物园参观，已知成人票每张20元，学生票每张10元．设门票的总费用为y元，则y＝________.

    10x＋20 【解析】根据总费用=成人票用钱数+学生票用钱数，可得y=10x+20. 故答案为：10x+20.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.3.2 用“角边角、角角边”判定三角形全等 同步练习 题型：解答题

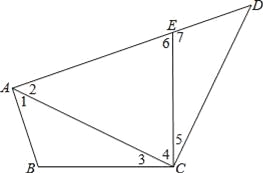
    如图，四边形ABCD中，E点在AD上，其中∠BAE=∠BCE=∠ACD=90°，且BC=CE，求证：△ABC与△DEC全等．

    证明过程见解析 【解析】试题分析：由∠BAE=∠BCE=∠ACD=90°，可求得∠DCE=∠ACB，且∠B+∠CEA=∠CEA+∠DEC=180°，可求得∠DEC=∠ABC，再结合条件可证明△ABC≌△DEC． 试题解析：∵∠BAE=∠BCE=∠ACD=90°，∴∠DCE+∠ECA=∠ECA+∠ACB， ∴∠DCE=∠ACB，且∠B+∠CEA=180°， 又∠DEC+∠CE...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.3.2 用“角边角、角角边”判定三角形全等 同步练习 题型：单选题

    如图所示，已知∠A＝∠D，∠1＝∠2，那么要得到△ABC≌△DEF，还应给出的条件是（ ）

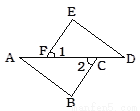
    A. ∠E＝∠B B. ED＝BC C. AB＝EF D. AF＝CD

    D 【解析】本题考查了全等三角形的判定 判定△ABC≌△DEF已经具备的条件是∠A=∠D，∠1=∠2，再加上两角的夹边对应相等，就可以利用ASA来判定三角形全等． ∵AF=CD ∴AC=DF 又∵∠A=∠D，∠1=∠2 ∴△ABC≌△DEF 故选D．

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级下册第三章3.2用关系式表示的变量间关系课时练习 题型：填空题

    函数y=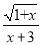中，自变量x的取值范围是 ．

    x≥－1． 【解析】 试题分析：函数自变量的范围一般从三个方面考虑：（1）当函数表达式是整式时，自变量可取全体实数；（2）当函数表达式是分式时，考虑分式的分母不能为0；（3）当函数表达式是二次根式时，被开方数为非负数． 根据二次根式的性质和分式的意义，被开方数大于等于0，可知：x+1≥0；分母不等于0，可知：x+3≠0，从而得出自变量x的取值范围即可．

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级下册第三章3.2用关系式表示的变量间关系课时练习 题型：单选题

    李大爷要围成一个矩形菜园，菜园的一边利用足够长的墙，用篱笆围成的另外三边总长度恰好为24米．要围成的菜园是如图所示的长方形ABCD．设BC边的长为x米，AB边的长为y米，则y与x之间的函数关系式是（　　）

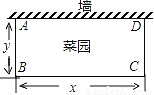
    A. y=-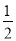x+12 B. y=﹣2x+24 C. y=2x﹣24 D. y=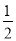x﹣12

    A 【解析】由题意可得： ，即： . 故选A.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下册达标检测 第二章 相交线与平行线 题型：解答题

    如图,已知AD∥BC,∠1=∠2,要说明∠3+∠4=180°,请补充完整解题过程,并在括号内填上相应的依据:

    解:因为AD∥BC(已知),

    所以∠1=∠3(___________).

    因为∠1=∠2(已知),

    所以∠2=∠3.

    所以BE∥___________ (___________). 

    所以∠3+∠4=180°(___________).

    证明见解析. 【解析】试题分析：根据平行线的判定和性质即可解决问题. 试题解析:因为AD∥BC(已知), 所以∠1=∠3(两直线平行,内错角相等). 因为∠1=∠2(已知), 所以∠2=∠3. 所以BE∥DF(同位角相等,两直线平行). 所以∠3+∠4=180°(两直线平行,同旁内角互补).

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下5.1 轴对称现象 同步练习 题型：解答题

    如图,把一张长方形纸片ABCD按图中的方式折叠,使点A与点E重合,点C与点F重合(E,F两点均在BD上),折痕分别为BH,DG.试说明:△BHE≌△DGF.

    见解析 【解析】试题分析：先根据矩形的性质得出∠ABD=∠BDC，再由图形折叠的性质得出∠ABH=∠EBH，∠FDG=∠CDG，∠A=∠HEB=90°，∠C=∠DFG=90°，进而可得出△BEH≌△DFG. 试题解析：∵四边形ABCD是长方形， ∴AB=CD，∠A=∠C=90°，∠ABD=∠BDC， ∵△BEH是△BAH翻折而成， ∴∠ABH=∠EBH，∠A=∠HEB...

    查看答案和解析>>

    同步练习册答案