
如果正n边形的一个外角是40°,则n的值为( )
A. 5 B. 6 C. 8 D. 9
D 【解析】∵n边形的外角和为360°, ∴正n边形的一个外角是 , ∴=40°, ∴n=9, 故选D.科目:初中数学 来源:人教版八年级下册数学全册综合测试卷 题型:单选题
下列函数中,变量y是x的反比例函数的是( )
A. y=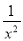 B. y=-
B. y=-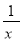 C. y=
C. y=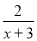 D. y=
D. y=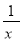 -1
-1
查看答案和解析>>
科目:初中数学 来源:人教版七年级下册 第1-3章 综合测试卷 题型:填空题
两条直线相交,交点的个数是________ ,两条直线平行,交点的个数是________ .
1 0 【解析】【解析】 两条直线相交,交点的个数是1,两条直线平行,交点的个数是0.故答案为:1,0.查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学全册综合测试卷 题型:填空题
已知等腰三角形的一腰上的高与底边的夹角为40度,那么它的顶角为________.
80° 【解析】如图, ①当顶角是钝角时,∠B=90°-40°=50°, ∴顶角=180°-2×50°=80°, ∵80°<90°, ∴顶角是80°不合题意,舍去; ②当顶角是锐角时,∠B=90°-40°=50°, ∠A=180°-2×50°=80°, 故答案为:80°.查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学全册综合测试卷 题型:填空题
平行四边形的两条邻边的比为2:1,周长为60cm,则这个四边形较短的边长为________.
10cm 【解析】设较短边长为xcm,则相邻的边长为2xcm,由题意则有 2(2x+x)=60, 解得:x=10, 故答案为:10cm.查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学全册综合测试卷 题型:单选题
在△ABC中,∠A=30°,∠B=50°,则∠C为( )
A. 30° B. 50° C. 80° D. 100°
D 【解析】∵在△ABC中,∠A=30°,∠B=50°, ∴∠C=180°-∠A-∠B=180°-30°-50°=100°, 故选D.查看答案和解析>>
科目:初中数学 来源:2017-2018学年度人教版九年级数学下册第26 章同步课时练习:26.2 实际问题与反比例函数(第2课时) 题型:解答题
学校准备在校园内修建一个矩形的绿化带,矩形的面积为定值,它的一边 y与另一边 x之间的函数关系式如下图所示.
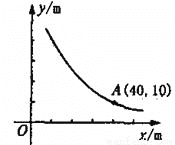
(1)绿化带面积是多少?你能写出这一函数表达式吗?
(2)完成下表,并回答问题:如果该绿化带的长不得超过40m,那么它的宽应控制在什么范围内?

查看答案和解析>>
科目:初中数学 来源:广东省2017-2018学年度九年级(上)数学第一次月考试卷(11月份)(解析版) 题型:填空题
如图△ABC中,边BC=12cm,高AD=6cm,边长为x的正方形PQMN的一边在BC上,其余两个顶点分别在AB、AC上,则正方形的边长x=_____cm.
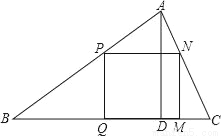
查看答案和解析>>
科目:初中数学 来源:江苏省无锡市2018届九年级上学期期末考试数学试卷 题型:解答题
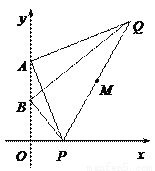
如图,A、B两点的坐标分别为(0,4),(0,2),点P为x轴正半轴上一动点,过点A作AP的垂线,过点B作BP的垂线,两垂线交于点Q,连接PQ,M为线段PQ的中点.
(1)求证:A、B、P、Q四点在以M为圆心的同一个圆上;
(2)当⊙M与x轴相切时,求点Q的坐标;
(3)当点P从点(1,0)运动到点(2,0)时,请直接写出线段QM扫过图形的面积.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com