
红红和娜娜按图示的规则玩“锤子、剪刀、布”游戏(如图),下列命题中错误的是( )


A.红红不是胜就是输,所以红红胜的概率为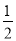
B.红红胜或娜娜胜的概率相等
C.两人出相同手势的概率为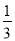
D.娜娜胜的概率和两人出相同手势的概率一样
科目:初中数学 来源:2017年初中毕业升学考试(重庆A卷)数学(解析版) 题型:选择题
下列图形都是由同样大小的菱形按照一定规律所组成的,其中第①个图形中一共有3个菱形,第②个图形中一共有7个菱形,第③个图形中一共有13个菱形,…,按此规律排列下去,第⑨个图形中菱形的个数为( )
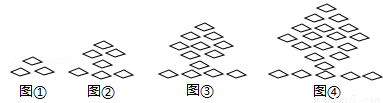
A.73 B.81 C.91 D.109
查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(浙江舟山卷)数学(解析版) 题型:选择题
下列关于函数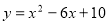 的四个命题:①当
的四个命题:①当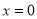 时,
时,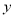 有最小值10;②
有最小值10;②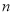 为任何实数,
为任何实数,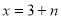 时的函数值大于
时的函数值大于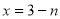 时的函数值;③若
时的函数值;③若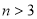 ,且
,且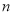 是整数,当
是整数,当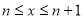 时,
时,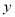 的整数值有
的整数值有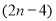 个;④若函数图象过点
个;④若函数图象过点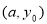 和
和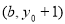 ,则
,则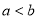 .其中真命题的序号是( )
.其中真命题的序号是( )
A.① B.② C.③ D.④
查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(浙江温州卷)数学(解析版) 题型:解答题
(本题14分)如图,已知线段AB=2,MN⊥AB于点M,且AM=BM,P是射线MN上一动点,E,D分别是PA,PB的中点,过点A,M,D的圆与BP的另一交点C(点C在线段BD上),连结AC,DE.
(1)当∠APB=28°时,求∠B和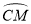 的度数;
的度数;
(2)求证:AC=AB。
(3)在点P的运动过程中
①当MP=4时,取四边形ACDE一边的两端点和线段MP上一点Q,若以这三点为顶点的三角形是直角三角形,且Q为锐角顶点,求所有满足条件的MQ的值;
②记AP与圆的另一个交点为F,将点F绕点D旋转90°得到点G,当点G恰好落在MN上时,连结AG,CG,DG,EG,直接写出△ACG和△DEG的面积之比.

查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(浙江温州卷)数学(解析版) 题型:填空题
小明家的洗手盆上装有一种抬启式水龙头(如图1),完全开启后,水流路线呈抛物线,把手端点A,出水口B和落水点C恰好在同一直线上,点A至出水管BD的距离为12cm,洗手盆及水龙头的相关数据如图2所示,现用高10.2cm的圆柱型水杯去接水,若水流所在抛物线经过点D和杯子上底面中心E,则点E到洗手盆内侧的距离EH为_________cm.
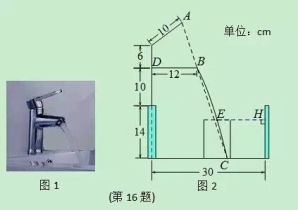
(第16题图)
查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(浙江台州卷)数学(解析版) 题型:解答题
交通工程学理论把在单向道路上行驶的汽车看成连续的流体,并用流量、速度、密度三个概念描述车流的基本特征,其中流量q(辆/小时)指单位时间内通过道路指定断面的车辆数;速度v(千米/小时)指通过道路指定断面的车辆速度,密度k(辆/千米)指通过道路指定断面单位长度内的车辆数.
为配合大数据治堵行动,测得某路段流量q与速度v之间关系的部分数据如下表:

(1)根据上表信息,下列三个函数关系式中,刻画q,v关系最准确的是 (只填上正确答案的序号)
①q=90v+100;②q=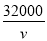 ;③
;③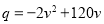 .
.
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速度为多少时,流量达到最大?最大流量是多少?
(3)已知q,v,k满足q=vk,请结合(1)中选取的函数关系式继续解决下列问题.
①市交通运行监控平台显示,当12≤v<18时道路出现轻度拥堵.试分析当车流密度k在什么范围时,该路段将出现轻度拥堵;
②在理想状态下,假设前后两车车头之间的距离d(米)均相等,求流量q最大时d的值.
查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(浙江绍兴卷)数学(解析版) 题型:选择题
下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差:
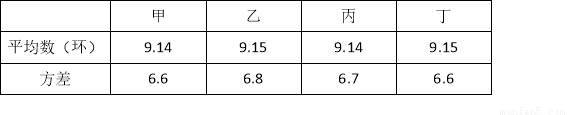
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( )
A.甲 B.乙 C.丙 D.丁
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com