
如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( )
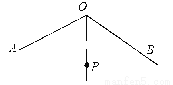
A. 2个 B. 3个 C. 4个 D. 无数个
D 【解析】如图在OA、OB上截取OE=OF=OP,作∠MPN=60°, ∵OP平分∠AOB,∴∠EOP=∠POF=60°, ∵OP=OE=OF,∴△OPE,△OPF是等边三角形, ∴EP=OP,∠EPO=∠OEP=∠PON=∠MPN=60°,∴∠EPM=∠OPN, 在△PEM和△PON中,∠PEM=∠PON,PE=PO,∠EPM=∠OPN, ∴△PEM≌△PO... 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:湖南省邵阳县2017-2018学年七年级上期末统一质量检测数学试卷 题型:单选题
下列换算中,错误的是( )
A. 83.5°=83°50′ B. 47.28°=47°16′48″
C. 16°5′24″=16.09° D. 0.25°=900″
A 【解析】试题解析: A. 故错误. 故选A.查看答案和解析>>
科目:初中数学 来源:新疆乌鲁木齐市2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
如图,将一副直角三角板如图放置,若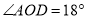 ,则
,则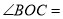 __度.
__度.
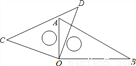
查看答案和解析>>
科目:初中数学 来源:黑龙江省哈尔滨市2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
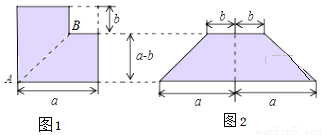
如图1所示,从边长为a的正方形纸片中减去一个边长为b的小正方形,再沿着线段AB剪开,把剪成的两张纸拼成如图2的等腰梯形(其面积= 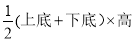 ).
).
(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2,请直接用含a、b的式子表示S1和S2;
(2)请写出上述过程所揭示的乘法公式.
查看答案和解析>>
科目:初中数学 来源:黑龙江省哈尔滨市2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
把多项式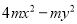 因式分解的结果是_______________.
因式分解的结果是_______________.
查看答案和解析>>
科目:初中数学 来源:黑龙江省哈尔滨市2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
下列图形中,是轴对称图形的是( )
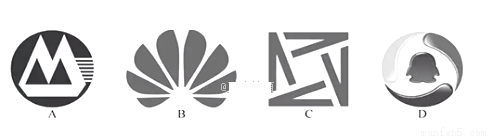
A. A B. B C. C D. D
B 【解析】A不是轴对称图形,故不符合题意;B是轴对称图形,故符合题意;C不是轴对称图形,故不符合题意;D不是轴对称图形,故不符合题意, 故选B.查看答案和解析>>
科目:初中数学 来源:江苏省东部分校2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
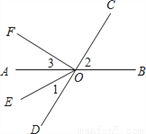
如图,直线 AB,CD 相交于点O,OE 平分∠AOD,OF⊥OC.
(1)图中∠AOF 的余角是 (把符合条件的角都填出来);
(2)如果∠AOC=130°36′,那么根据 ,可得∠BOD= °;
(3)如果∠1与∠3的度数之比为3:4,求∠EOC和∠2的度数.
查看答案和解析>>
科目:初中数学 来源:江苏省东部分校2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
数轴上表示一个数的点与原点的距离是6,那么这个数是_______.
±6 【解析】【解析】 ∵|±6|=6,∴数轴上表示一个数的点与原点的距离是6,那么这个数是±6.故答案为:±6.查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
(1)计算: 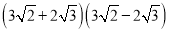 ; (2)解方程:
; (2)解方程: 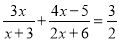 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com