
如图,分别以△ABC的两边AB、AC向外作正方形ABGF和ACDE,作AH⊥BC于H,HA的延长线交FE于M,求证:FM=ME.

|
分析:不易直接证明.分别从E、F作HM的垂线EP、FQ,垂足分别是P、Q,若能证得EP=FQ,便能通过△EPM≌△FQM得出FM=ME.充分利用四边形ABGF、四边形ACDE都为正方形这一条件便能完成证明. 证明:作EP⊥HM于P,FQ⊥HM的延长线于Q ∵四边形ACDE是正方形,∠CAE=90° ∴∠1+∠EAP=90°, ∵∠2+∠EAP=90°, ∴∠1=∠2, 又∠AHC=∠EPA=90°,AC=EA, ∴△ACH≌△EAP, ∴EP=AH. 同理 FQ=AH. ∴EP=FQ. 又∠FMQ=∠EMP,∠Q=∠MPE=90°, ∴△FQM≌△EPM. ∴FM=ME. |


科目:初中数学 来源: 题型:
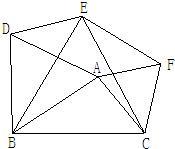 20、如图,分别以△ABC的三边为边在BC的同侧作三个等边三角形,即△ABD,△BCE,△ACF.请回答下列问题:
20、如图,分别以△ABC的三边为边在BC的同侧作三个等边三角形,即△ABD,△BCE,△ACF.请回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,分别以△ABC的边AB,AC向外作等边三角形ABD和等边三角形ACE,线段BE与CD相交于点O,连接OA.
如图,分别以△ABC的边AB,AC向外作等边三角形ABD和等边三角形ACE,线段BE与CD相交于点O,连接OA.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com