练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，∠COD=116°，∠BOD=90°，OA平分∠BOC，求∠AOD的度数．

    解：∵∠COD=116°，∠BOD=90°，
    ∴∠BOC=∠COD-∠BOD=116°-90°=26°，
    又∵OA平分∠BOC，
    ∴∠AOB=∠BOC=×26=13°，
    ∴∠AOD=∠BOD+∠AOB=90°+13°=103°．
    ∴∠AOD的度数是103°．
    故答案为103°．
    分析：由角平分线的定义，结合角的运算，易求∠AOD的度数．
    点评：根据角平分线定义得出所求角与已知角的关系转化求解．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图1，射线OC、OD在∠AOB的内部，且∠AOB=150°，∠COD=30°，射线OM、ON分别平分∠AOD、∠BOC，
    （1）求∠MON的大小，并说明理由；
    （2）如图2，若∠AOC=15°，将∠COD绕点O以每秒x°的速度逆时针旋转10秒钟，此时∠AOM：∠BON=7：11，如图3所示，求x的值．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

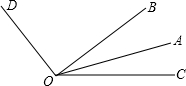
    如图的扇形统计图表示的是120名同学某次体育测试的成绩，分为甲等，乙等，丙等和丁等，OA⊥OD，∠COD=54°，∠AOB=∠BOC，回答下列问题：
    （1）该统计图各个扇形所占百分比的和为
    1
    1
    ；
    （2）∠BOC=
    108°
    108°
    ；
    （3）体育成绩为乙等的学生占总数的
    30
    30
    %；
    （4）体育成绩为甲等的学生有
    30
    30
    名．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，∠AOB与∠COD都是直角，若∠BOC：∠AOD=7：11，求∠AOC的度数．

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年四川省成都市七年级上学期期末模拟数学试卷（解析版） 题型：解答题

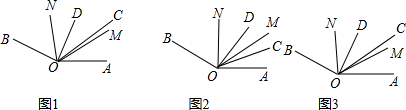
    如图1，射线OC、OD在∠AOB的内部，且∠AOB=150°，∠COD=30°，射线OM、ON分别平分∠AOD、∠BOC，

    （1）求∠MON的大小，并说明理由；

    （2）如图2，若∠AOC=15°，将∠COD绕点O以每秒x°的速度逆时针旋转10秒钟，此时∠AOM︰∠BON=7︰11，如图3所示，求x的值．

     

    查看答案和解析>>

    科目：初中数学 来源：2011年初中毕业升学考试（福建漳州卷）数学 题型：解答题

    （11·漳州）（满分10分）如图，AB是⊙O的直径，，∠COD＝60°．

    （1）△AOC是等边三角形吗？请说明理由；

    （2）求证：OC∥BD．

     

     

     

     

     

     

    查看答案和解析>>

    同步练习册答案