
若方程组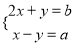 的解是
的解是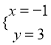 ,则直线y=-2x+b与直线y=x-a的交点坐标是______.
,则直线y=-2x+b与直线y=x-a的交点坐标是______.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017年广东省韶关市南雄市中考数学模拟试卷 题型:单选题
已知二次函数y=ax2+bx+c的图象如图所示,则a、b、c满足( )
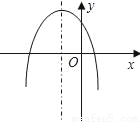
A. a<0,b<0,c>0 B. a<0,b<0,c<0 C. a<0,b>0,c>0 D. a>0,b<0,c>0
A 【解析】试题分析:由于开口向下可以判断a<0,由与y轴交于正半轴得到c>0,又由于对称轴x=-<0,可以得到b<0,所以可以找到结果. 试题解析:根据二次函数图象的性质, ∵开口向下, ∴a<0, ∵与y轴交于正半轴, ∴c>0, 又∵对称轴x=-<0, ∴b<0, 所以A正确.查看答案和解析>>
科目:初中数学 来源:山东省德州市2017-2018学年九年级上学期期中考试数学试卷 题型:解答题
解方程:① 5 x2-4x-12=0 ② 2x2-12x+5=0(配方法)
①x1=2 ,x2=-;②. 【解析】试题分析:(1)分解因式得出(x-2)(5x+6)=0,推出方程x-2=0,5x+6=0,求出方程的解即可; (2)先把常数移到右侧,再把二次项系数化为1,两边同时加上一次项系数一半的平方,配方成完全平方,两边开方,即可求得方程的解. 试题分析:①5x2-4x-12=0, (x-2)(5x+6)=0, x-2=0或5x+6=0, ...查看答案和解析>>
科目:初中数学 来源:山东省德州市2017-2018学年九年级上学期期中考试数学试卷 题型:单选题
如图,所给图形中是中心对称图形但不是轴对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 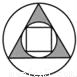
查看答案和解析>>
科目:初中数学 来源:2018年春人教版八年级数学下册(广西)期末测试 题型:解答题
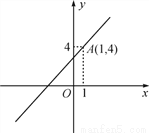
如图,已知,一次函数y=kx+3的图象经过点A(1,4).
(1)求这个一次函数的解析式;
(2)试判断点B(-1,5),C(0,3),D(2,1)是否在这个一次函数的图象上.
查看答案和解析>>
科目:初中数学 来源:2018年春人教版八年级数学下册(广西)期末测试 题型:单选题
某中学组织初一、初二学生举行“四城同创”宣传活动,从学校坐车出发,先上坡到达A地后,宣传8分钟;然后下坡到B地宣传8分钟返回,行程情况如图.若返回时,上、下坡速度保持不变,在A地仍要宣传8分钟,则他们从B地返回学校用的时间是( )
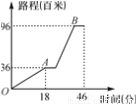
A. 48分钟 B. 45.2分钟 C. 46分钟 D. 33分钟
B 【解析】由上图可知,上坡的路程为3600米,速度为200米每分钟;下坡时的路程为6000米,速度为6000÷(46-18-8×2)=500米每分钟;由于返回时上下坡互换,变为上坡路程为6000米,所以所用时间为6000÷200=30分钟;下坡路程为3600米,所用时间是3600÷500=7.2分钟;又知在A地停8分钟;所以总时间为30+8+7.2=45.2分钟.故选B查看答案和解析>>
科目:初中数学 来源:2018年春人教版八年级数学下册(广西)期末测试 题型:单选题
下列计算错误的是( )
A. 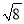 -
-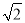 =
=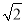 B.
B. 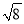 ÷2=
÷2=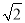
C. 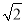 ×
×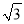 =
=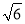 D. 3+2
D. 3+2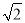 =5
=5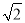
查看答案和解析>>
科目:初中数学 来源:江西省2017-2018学年度八年级第三次月考数学试卷 题型:填空题
已知0<2x-1<1,则x的解集为_________
【解析】根据不等式得基本性质1,不等式的两边同加上1可得,1<2x<2, 再根据不等式得基本性质2,不等式的两边同除以2可得, , 所以不等式组的解集为.查看答案和解析>>
科目:初中数学 来源:山西省2017-2018学年八年级上期末模拟数学试卷 题型:解答题
如图,在?ABCD中,M,N在对角线AC上,且AM=CN,求证:BM∥DN.
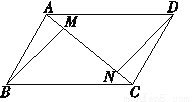
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com