
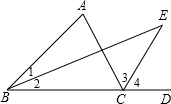
 如图:∠ACD是△ABC的外角,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E.
如图:∠ACD是△ABC的外角,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E. ∠A.
∠A.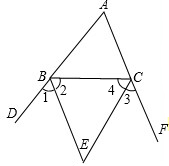 (1)证明:∵∠ACD=∠A+∠ABC,
(1)证明:∵∠ACD=∠A+∠ABC, (∠A+∠ABC).
(∠A+∠ABC). (∠A+∠ABC).
(∠A+∠ABC). ∠ABC,
∠ABC, ∠ABC+∠E=
∠ABC+∠E= (∠A+∠ABC),
(∠A+∠ABC), ∠A;
∠A; ∠CBD,∠4=
∠CBD,∠4= ∠BCF,
∠BCF, (∠A+∠ACB),∠4=
(∠A+∠ACB),∠4= (∠A+∠ABC).
(∠A+∠ABC). (∠A+∠ACB)+
(∠A+∠ACB)+ (∠A+∠ABC)=180°,即∠E+
(∠A+∠ABC)=180°,即∠E+ ∠A+
∠A+ (∠A+∠ACB+∠ABC)=180°.
(∠A+∠ACB+∠ABC)=180°. ∠A=90°.
∠A=90°. (∠A+∠ABC),∠2=
(∠A+∠ABC),∠2= ∠ABC,利用等量代换,即可求得∠A与∠E的关系;
∠ABC,利用等量代换,即可求得∠A与∠E的关系; ∠CBD,∠4=
∠CBD,∠4= ∠BCF,由三角形外角的性质可知,∠CBD=∠A+∠ACB,∠BCF=∠A+∠ABC,由角平分线的定义可知,∠2=
∠BCF,由三角形外角的性质可知,∠CBD=∠A+∠ACB,∠BCF=∠A+∠ABC,由角平分线的定义可知,∠2= (∠A+∠ACB),∠4=
(∠A+∠ACB),∠4= (∠A+∠ABC),根据三角形定理可知∠E+∠2+∠4=180°,故可得出∠E+
(∠A+∠ABC),根据三角形定理可知∠E+∠2+∠4=180°,故可得出∠E+ ∠A+
∠A+ (∠A+∠ACB+∠ABC)=180°,再由∠A+∠ACB+∠ABC=180°即可得出结论.
(∠A+∠ACB+∠ABC)=180°,再由∠A+∠ACB+∠ABC=180°即可得出结论.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
 21、如图,∠ACD是△ABC的一个外角,请你从下面三个条件中,选出两个作为已知条件,另一个作为结论,推出一个正确的命题.
21、如图,∠ACD是△ABC的一个外角,请你从下面三个条件中,选出两个作为已知条件,另一个作为结论,推出一个正确的命题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com