
 16、如图,已知:△ARC的外角∠CAG=120°,∠CAG的平分线AD与BC的延长线相交于点D,延长DA与.△ABC的外接圆交于点F,连接FB、FC,FC与AB相交于点E.
16、如图,已知:△ARC的外角∠CAG=120°,∠CAG的平分线AD与BC的延长线相交于点D,延长DA与.△ABC的外接圆交于点F,连接FB、FC,FC与AB相交于点E.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
现场学习:我们知道,若锐角α的三角函数值为sinα = m,则可通过计算器得到角α的大小,这时我们用arc sin m来表示α,记作:α=arc sin m;若cos α = m,则记α =arc cos m;若tan α = m,则记α = arc tan m.
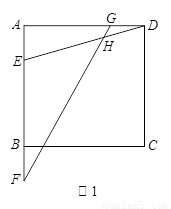
解决问题:如图,已知正方形ABCD,点E是边AB上一动点,点F在AB边或其延长线上,点G在边AD上.连结ED,FG,交点为H.
(1)如图1,若AE=BF=GD,请直接写出∠EHF= °;
 (2)如图2,若EF =
(2)如图2,若EF =![]() CD,GD=
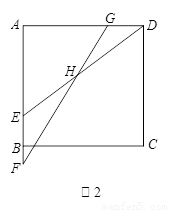
CD,GD=![]() AE,设∠EHF=α.请判断当点E在AB上运动时, ∠EHF的大小是否发生变化?若发生变化,请说明理由;若不发生变化,请求出α.
AE,设∠EHF=α.请判断当点E在AB上运动时, ∠EHF的大小是否发生变化?若发生变化,请说明理由;若不发生变化,请求出α.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2)如图2,若EF=
(2)如图2,若EF= CD,GD=
CD,GD= AE,设∠EHF=α.请判断当点E在AB上运动时, ∠EHF的大小是否发生变化?若发生变化,请说明理由;若不发生变化,请求出α.
AE,设∠EHF=α.请判断当点E在AB上运动时, ∠EHF的大小是否发生变化?若发生变化,请说明理由;若不发生变化,请求出α. 查看答案和解析>>
科目:初中数学 来源:江苏省苏州市高新区2012届八年级下学期期末考试数学试题 题型:解答题
现场学习:我们知道,若锐角α的三角函数值为sinα = m,则可通过计算器得到角α的大小,这时我们用arc sin m来表示α,记作:α=arc sin m;若cos α = m,则记α = arc cos m;若tan α = m,则记α = arc tan m.
解决问题:如图,已知正方形ABCD,点E是边AB上一动点,点F在AB边或其延长线上,点G在边AD上.连结ED,FG,交点为H.
(1)如图1,若AE=BF=GD,请直接写出∠EHF= °;
 (2)如图2,若EF =
(2)如图2,若EF =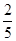 CD,GD=
CD,GD=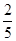 AE,设∠EHF=α.请判断当点E在AB上运动时, ∠EHF的大小是否发生变化?若发生变化,请说明理由;若不发生变化,请求出α.
AE,设∠EHF=α.请判断当点E在AB上运动时, ∠EHF的大小是否发生变化?若发生变化,请说明理由;若不发生变化,请求出α.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com