
 如图所示,是城市部分街道示意图,AB=BC=AC,CD=CE=DE,A,B,C,D,E,F,G,H为“公共汽车”停靠点.“公共汽车甲”从A站出发,按照A,H,G,D,E,C,F的顺序到达F站,“公共汽车乙”从B站出发,按照B,F,H,E,D,C,G的顺序到达G站.如果甲.乙两车分别从A,B两站同时出发,在各站耽误的时间相同,两车速度也一样,试问哪一辆公共汽车先到达指定站,为什么?
如图所示,是城市部分街道示意图,AB=BC=AC,CD=CE=DE,A,B,C,D,E,F,G,H为“公共汽车”停靠点.“公共汽车甲”从A站出发,按照A,H,G,D,E,C,F的顺序到达F站,“公共汽车乙”从B站出发,按照B,F,H,E,D,C,G的顺序到达G站.如果甲.乙两车分别从A,B两站同时出发,在各站耽误的时间相同,两车速度也一样,试问哪一辆公共汽车先到达指定站,为什么?
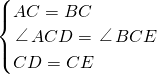



科目:初中数学 来源: 题型:
 21、如图所示,是城市部分街道示意图,AB=BC=AC,CD=CE=DE,A,B,C,D,E,F,G,H为“公共汽车”停靠点.“公共汽车甲”从A站出发,按照A,H,G,D,E,C,F的顺序到达F站,“公共汽车乙”从B站出发,按照B,F,H,E,D,C,G的顺序到达G站.如果甲.乙两车分别从A,B两站同时出发,在各站耽误的时间相同,两车速度也一样,试问哪一辆公共汽车先到达指定站,为什么?
21、如图所示,是城市部分街道示意图,AB=BC=AC,CD=CE=DE,A,B,C,D,E,F,G,H为“公共汽车”停靠点.“公共汽车甲”从A站出发,按照A,H,G,D,E,C,F的顺序到达F站,“公共汽车乙”从B站出发,按照B,F,H,E,D,C,G的顺序到达G站.如果甲.乙两车分别从A,B两站同时出发,在各站耽误的时间相同,两车速度也一样,试问哪一辆公共汽车先到达指定站,为什么?查看答案和解析>>
科目:初中数学 来源:101网校同步练习 初三数学 华东师大(新课标2001/3年初审) 华东师大版 题型:044
(应用题)如图所示,是城市部分街道示意图,AB=BC=AC,CD=CE=DE,A、B、C、D、E、F、G为“公共汽车”停靠点,“甲公共汽车”从A站出发,按照A、H、G、D、E、C、F的顺序到达F站,“乙公共汽车”从B站出发,沿B、F、H、E、D、C、G的顺序到达G站.如果甲、乙分别同时从A、B站出发,在各站耽误的时间相同,两车速度也一样,试问哪一辆公共汽车先到达指定站?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,某城市部分街道示意图,AF∥BC,EC⊥BC,BA∥DE,BD∥AE,EF=FC,甲、乙两人同时从B站乘车到F站,甲乘1路车,路线是B→A→E→F,乙乘2路,路线是B→D→C→F,假设两车速度相同,途中耽误时间相同,那么谁先到达F站,请说明理由.
 |
查看答案和解析>>
科目:初中数学 来源:《第1章 证明(二)》2009年单元测试(1)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com