练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图已知，矩形ABCD，DE平分∠ADC，∠BDE=15°，求：∠COE的度数．

    答案：略
    解析：

    解：∵矩形ABCD，∴∠ADC=∠DCB=90°，

    OD=BD，OC=AC，BD=AC，

    ∴OD=OC，∠EDC＋∠DEC=90°．

    ∵DE平分∠ADC，∴∠EDC=45°，

    ∴∠DEC=45°=∠EDC，从而CE=CD．

    ∵∠BDE=15°，∴∠BDC=45°+15°=60°．

    ∴△ODC是等边三角形，于是OC=CD=CE，∠DCO=60°．

    ∴∠OCE=90°－60°=30°．

    ∵∠COE=∠CEO，∠COE＋∠CEO＋∠OCE=180°，

    ∴2∠COE=150°，即∠COE=75°．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网如图已知AB为⊙O的直径，弦AC∥BD，连接AD与BC．
    （1）求证：四边形ADBC是矩形；
    （2）若∠ABC=30°，⊙O的半径是20厘米，求任意投掷一枚飞镖落在矩形区域内的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•嘉定区一模）如图已知△ABC中AB=AC=10，BC=16，矩形DEFG的边EF在△ABC的边BC上，顶点D、G分别在AB、AC上，设DE的长为x，矩形DEFG的面积为y，求y关于x的函数关系式，并写出这个函数的定义域．

    查看答案和解析>>

    科目：初中数学 来源：鼎尖助学系列—同步练习(数学 八年级下册)、函数及其图象　画相似图形 题型：044

    如图已知锐角三角形ABC，求作矩形MNPQ，使NP在BC上，点M和点Q分别AB、AC上，且使MN：NP=1：2．

    作法：①在AB上取一点，作，垂足为；

    ②在BC(或其延长线)上取一点，使；

    ③以和为邻边作矩形；

    ④作射线交AC于Q；

    ⑤作交BC于P，作QM∥BC交AB于M，作交BC于N，则四边形MNPQ为所求作的矩形．

    ⑥回答：四边形MNPQ为什么是所求作的矩形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

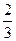    (满分l4分)如图已知直线l1:y=x+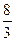与直线l2:y=2x+16相交于点C，l1，l2分别交x轴于A，B两点．矩形DEFG的顶点D，E分别在直线l1，l2上，顶点F，G都在X轴上，且点G与点B重合．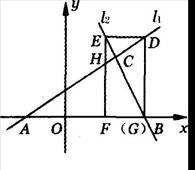
    (1)求△ABC的面积；
    (2)求矩形DEFG的边DE与EF的长；
    (3)若此时矩形DEFG，沿x轴的反方向以每秒l个单位长度的速度平移，设移动时间为t 5(0≤t≤12)，矩形DEFG与△ABC重叠部分的面积为S，求S关于t的函数关系式，并写出相应的t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源：2010年浙江省初中毕业生学业考试模拟试卷数学卷 题型：解答题

    (满分l4分)如图已知直线l1:y=x+与直线l2:y=2x+16相交于点C，l1，l2分别交x轴于A，B两点．矩形DEFG的顶点D，E分别在直线l1，l2上，顶点F，G都在X轴上，且点G与点B重合．
    (1)求△ABC的面积；
    (2)求矩形DEFG的边DE与EF的长；
    (3)若此时矩形DEFG，沿x轴的反方向以每秒l个单位长度的速度平移，设移动时间为t 5(0≤t≤12)，矩形DEFG与△ABC重叠部分的面积为S，求S关于t的函数关系式，并写出相应的t的取值范围．

    查看答案和解析>>

    同步练习册答案