
解:(1)∵直线y=x+b与x轴交于点C(4,0),
∴把点C(4,0)代入y=x+b得:b=-4,
∴直线的解析式是:y=x-4;
∵直线也过A点,
∴把A点代入y=x-4得到:n=-5
∴A(-1,-5),
把将A点代入

(x<0)得:m=5,
∴双曲线的解析式是:y=

;
(2)过点O作OM⊥AC于点M,
∵B点经过y轴,
∴x=0,
∴0-4=y,
∴y=4,
∴B(0,-4),
AO=

=
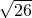
,
∵OC=OB=4,
∴△OCB是等腰三角形,
∴∠OBC=∠OCB=45°,
∴在△OMB中 sin45°=
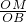
=
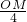
,
∴OM=2

,
∴在△AOM中,
sin∠OAB=
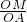

=

;
(3)存在;
过点A作AN⊥y轴,垂足为点N,
则AN=1,BN=1,
则AB=

=

,
∵OB=OC=4,
∴BC=
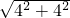
=4

,
∠OBC=∠OCB=45°,
∴∠OBA=∠BCD=135°,
∴△OBA∽△BCD或△OBA∽△DCB,
∴
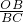
=

或
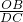
=
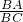
,
∴

=

或

=
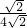
,
∴CD=2或CD=16,
∴点D的坐标是(6,0)或(20,0).
分析:(1)把点C的坐标代入y=x+b,求出b的值,得出直线的解析式;把点A(-1,n)代入y=x-4得到n的值,求出A点的坐标,再把将A点代入

(x<0)中,求出m的值,从而得出双曲线的解析式;
(2)先过点O作OM⊥AC于点M,根据B点经过y轴,求出B点的坐标,根据勾股定理求出AO的值,根据OC=OB=4,得出△OCB是等腰三角形,求出∠OBC=∠OCB的度数,再在△OMB中,根据正弦定理求出OM的值,从而得出∠OAB的正弦值.
(3)先过点A作AN⊥y轴,垂足为点N,根据AN=1,BN=1,求出AB的值,根据OB=OC=4,求出BC的值,再根据∠OBC=∠OCB=45°,得出∠OBA=∠BCD,从而得出△OBA∽△BCD或△OBA∽△DCB,最后根据
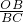
=

或
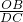
=
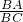
,再代入求出CD的长,即可得出答案.
点评:此题考查了反比例函数的综合,用到的知识点是勾股定理、相似三角形的判断与性质,特殊角的三角函数值,关键是根据题意作出辅助线,求出线段的长度.

 直线y=x+b与x轴交于点C(4,0),与y轴交于点B,并与双曲线
直线y=x+b与x轴交于点C(4,0),与y轴交于点B,并与双曲线 (x<0)交于点A(-1,n).
(x<0)交于点A(-1,n). 解:(1)∵直线y=x+b与x轴交于点C(4,0),
解:(1)∵直线y=x+b与x轴交于点C(4,0), (x<0)得:m=5,
(x<0)得:m=5, ;
; =
=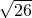 ,
,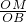 =
=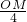 ,
, ,
,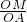
 =
= ;
; =
= ,
,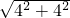 =4
=4 ,
,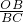 =
= 或
或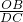 =
=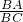 ,
, =
= 或
或 =
=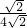 ,
, (x<0)中,求出m的值,从而得出双曲线的解析式;
(x<0)中,求出m的值,从而得出双曲线的解析式;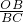 =
= 或
或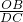 =
=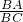 ,再代入求出CD的长,即可得出答案.
,再代入求出CD的长,即可得出答案.

 (2012•兰州)如图,M为双曲线y=
(2012•兰州)如图,M为双曲线y=