练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图所示，有两个正方形花坛，准备把每个花坛都分割成形状相同的四块，种植不同的花草．下面左边的两个图案是设计示例，请你在右边的两个正方形中再设计两个不同的图案．

    答案：
    解析：

    　　解：如图所示．

    　　说明：本题是利用轴对称的性质设计图案的实际应用题，主要考查学生分析、解决实际问题的能力．


    提示：

    提示：发挥想像，按要求设计图案．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    1、（1）如图，平面内两条互相
    垂直
    并且原点
    重合
    的
    数轴
    组成平面直角坐标系．其中，水平的数轴称为
    x轴
    或
    横轴
    ，习惯上取
    向右方向
    为正方向；竖直的数轴称为
    y轴
    或
    纵轴
    ，取
    向上方向
    为正方向；两坐标轴的交点叫做平面直角坐标系的
    原点
    ．直角坐标系所在的
    平面
    叫做坐标平面．

    （2）有了平面直角坐标系，平面内的点就可以用一个
    有序数对
    来表示．如果有序数对（a，b）表示坐标平面内的点A，那么有序数对（a，b）叫做
    A点的坐标
    ．其中，a叫做A点的
    横坐标
    ；b叫做A点的
    纵坐标
    ．
    （3）建立了平面直角坐标系以后，坐标平面就被
    两条坐标轴
    分成了Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分，如图所示，分别叫做
    第一象限
    、
    第二象限
    、
    第三象限
    、
    第四象限
    ．注意
    坐标轴上的点
    不属于任何象限．

    （4）坐标平面内，点所在的位置不同，它的坐标的符号特征如下：（请用“+”、“-”、“0”分别填写）

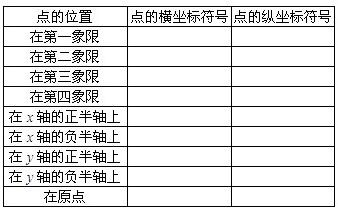
    查看答案和解析>>

    科目：初中数学 来源： 题型：

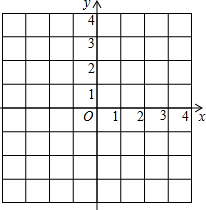    如图，平面直角坐标系中的方格阵表示一个纵横交错的街道模型的一部分，以O为原点，建立如图所示的平面直角坐标系，x轴，y轴的正方向分别表示正东、正北方向，出租车只能沿街道（网格线）行驶，且从一个路口（格点）到另一个路口，必须选择最短路线，称最短路线的长度为两个街区之间的“出租车距离”．设图中每个小正方形方格的边长为1个单位．可以发现：
    从原点O到（2，-1）的“出租车距离”为3，最短路线有3条；
    从原点O到（2，2）的“出租车距离”为4，最短路线有6条．
    （1）①从原点O到（6，1）的“出租车距离”为
    7
    7
    ．最短路线有
    7
    7
    条；
    ②与原点O的“出租车距离”等于30的路口共有
    120
    120
    个．
    （2）①解释应用：从原点O到坐标（n，2）（n为大于2的整数）的路口A，有多少条最短路线？（请给出适当的说理或过程）
    ②解决问题：
    从坐标为（1，-2）的路口到坐标为（3，36）的路口，最短路线有
    780
    780
    条．

    查看答案和解析>>

    科目：初中数学 来源：2014届江苏泰兴济川中学七年级上期期末考试数学试卷（解析版） 题型：解答题

    在平整的地面上，有若干个完全相同棱长的小正方体堆成一个几何体，如图所示。

    (1) 请画出这个几何体的三视图。

     

     

     

     

          主视图               左视图               俯视图

    (2) 如果在这个几何体的表面喷上黄色的漆，则在所有的小正方体中，有      个正方体只有一个面是黄

    色，有      个正方体只有两个面是黄色，有      个正方体只有三个面是黄色。

    (3) 若现在你手头还有一些相同的小正方体，如果保持俯视图和左视图不变，最多可以再添加几个小正方

    体？

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    （1）如图，平面内两条互相______并且原点______的______组成平面直角坐标系．其中，水平的数轴称为______或______，习惯上取______为正方向；竖直的数轴称为______或______，取______为正方向；两坐标轴的交点叫做平面直角坐标系的______．直角坐标系所在的______叫做坐标平面．

    （2）有了平面直角坐标系，平面内的点就可以用一个______来表示．如果有序数对（a，b）表示坐标平面内的点A，那么有序数对（a，b）叫做______．其中，a叫做A点的______；b叫做A点的______．
    （3）建立了平面直角坐标系以后，坐标平面就被______分成了Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分，如图所示，分别叫做______、______、______、______．注意______不属于任何象限．

    （4）坐标平面内，点所在的位置不同，它的坐标的符号特征如下：（请用“+”、“-”、“0”分别填写）

    查看答案和解析>>

    科目：初中数学 来源：2009年安徽省合肥市一中高一自主招生考试数学试卷（解析版） 题型：解答题

    如图，平面直角坐标系中的方格阵表示一个纵横交错的街道模型的一部分，以O为原点，建立如图所示的平面直角坐标系，x轴，y轴的正方向分别表示正东、正北方向，出租车只能沿街道（网格线）行驶，且从一个路口（格点）到另一个路口，必须选择最短路线，称最短路线的长度为两个街区之间的“出租车距离”．设图中每个小正方形方格的边长为1个单位．可以发现：
    从原点O到（2，-1）的“出租车距离”为3，最短路线有3条；
    从原点O到（2，2）的“出租车距离”为4，最短路线有6条．
    （1）①从原点O到（6，1）的“出租车距离”为______．最短路线有______条；
    ②与原点O的“出租车距离”等于30的路口共有______个．
    （2）①解释应用：从原点O到坐标（n，2）（n为大于2的整数）的路口A，有多少条最短路线？（请给出适当的说理或过程）
    ②解决问题：
    从坐标为（1，-2）的路口到坐标为（3，36）的路口，最短路线有______条．

    查看答案和解析>>

    同步练习册答案