Question

在平面直角坐标系xOy中，抛物线y=mx²-2mx+n与x轴交于A、B两点，点A的坐标为（-2，0）．
（1）求B点坐标；
（2）直线经过点B．
①求直线和抛物线的解析式；
②点P在抛物线上，过点P作y轴的垂线l，垂足为D（0，d）．将抛物线在直线l上方的部分沿直线l翻折，图象的其余部分保持不变，得到一个新图象G．请结合图象回答：当图象G与直线只有两个公共点时，d的取值范围是______．

Answer 1

解：（1）依题意，可得抛物线的对称轴为：x=-=1．
∵抛物线与x轴交于A、B两点，点A的坐标为（-2，0），
∴点B的坐标为 （4，0）；

（2）①

∵点B在直线上，
∴0=2+4m+n  1)．
∵点A在二次函数y=mx²-2mx+n的图象上，
∴0=4m+4m+n  2)．
由1)、2)可得m=，n=-4．
∴抛物线的解析式为y=，直线的解析式为y=． 

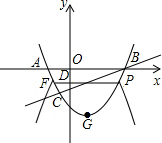②翻折图象即是FDP直线下方的图象．要使得直线y=x-2与新图象G仅有两个交点，须保证点P在直线下方，而点F在直线上方．
最低点G（1，-）．点D为（0，d），把-≤y=d＜0代入原抛物线方程y=x²-x-4=d，
解得：x₁=1-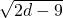，即点F的横坐标，
x₂=1+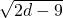，即点P的横坐标
所以：d＞y₁=x₁-2=（1-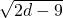）-2，即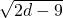：＞-（2d+3）…（a）
d＜y₂=x₂-2=（1+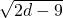）-2，即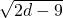：＞2d+3…（b）
当2d+3≤0即-≤d≤-时，（b）成立，（a）两边平方整理得：
2d²+5d＜0，解得：-＜d＜-；
当2d+3≥0即-≤d＜0时，（a）成立，（b）两边平方整理得：
2d²+5d＜0，解得：-≤d＜0
综上所述：-＜d＜0．

分析：（1）先根据对称轴公式求得抛物线的对称轴为：x=-=1．依此即可求得B点坐标；
（2）①将B点坐标分别代入抛物线y=mx²-2mx+n和直线，得到关于m，n的方程组，求得m，n的值，从而得到直线和抛物线的解析式；
②要使得直线y=x-2与新图象G仅有两个交点，须保证点P在直线下方，而点F在直线上方，分析即可求解．
点评：本题是一道一次函数与二次函数的综合试题，考查了二次函数与坐标轴的交点坐标的运用，轴对称的性质的运用，解答时根据函数之间的关系建立方程是解答本题的关键．