练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    判断：三角形的中线小于任何一个边. （　　 ）

     

    答案：F
    提示：

    		这是不一定的，可以通过画图进行简单论证

     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

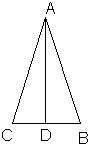    22、我们知道一个图形的性质和判定之间有着密切的联系．比如，由等腰三角形的性质“等边对等角”很易得到它的判定“等角对等边”．小明在学完“等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合”性质后，得到如下三个猜想：
    （1）如果一个三角形一边的中线和这边上的高相互重合，则这个三角形是等腰三角形；
    （2）如果一个三角形一边的高和这边所对的角的平分线相互重合，则这个三角形是等腰三角形；
    （3）如果一个三角形一边的中线和这边所对的角的平分线相互重合，则这个三角形是等腰三角形．
    我们运用线段垂直平分线的性质，很易证明猜想（1）的正确性．现请你帮助小明判断他的猜想（2）、（3）是否成立，若成立，请结合图形，写出已知、求证和证明过程；若不成立，请举反例说明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

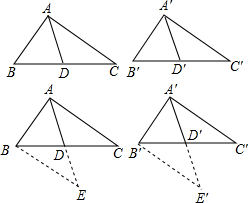    （2013•莒南县一模）【典型练习】如果两个三角形有两条边和其中一边上的中线对应相等，那么这两个三角形全等．（无需证明）
    【拓展变式】小明很顺利的完成了上面的练习后，又进一步对该命题进行了发散思维，把原命题中的一些条件进行了变换，得到了如下三个不同的命题：
    （1）如果两个三角形有两条边和第三边上的中线对应相等，那么这两个三角形全等．
    （2）如果两个三角形有两条边和第三边上的高对应相等，那么这两个三角形全等．
    （3）如果两个三角形有两条边和夹角的平分线对应相等，那么这两个三角形全等．
    【探索新知】小明对这三个命题，无法判断其命题的真假，于是他向老师求教．数学老师对命题（1）做出了一些指导，请你帮助小明完成下面的解答过程．
    已知：如图，AB=A′B′，AD=A′D′，AD是BC边上的中线，A′D′是B′C′边上的中线，求证：△ABC≌△A′B′C′，
    证明：如图，延长AD至E使AD=DE，连接BE，延长A′D′至E′使A′D′=D′E′，连接B′E′．
    【合作学习】对于命题（2）、（3），你能帮助小明判断命题的真假吗？如果是真命题，请给完整的证明，如果是假命题，在下面的空白处做出解答．（要求：画出图形，说明理由．）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

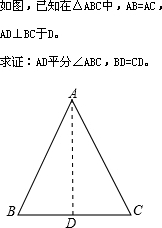    小明在证明“等腰三角形底边上的高线、底边上的中线和顶角的平分线互相重合”这一命题时，画出图形，写出“已知”、“求证”（如图）．
    （1）请你帮助小明完成证明过程．
    （2）请你作出判断：小明写出的“已知”、“求证”是否完整？在横线上填“是”或“否”．
    是
    是

    （3）做完（1）后，小明模仿老师上课时的方法，又提出了如下几个问题：
    如：①若将题中“AD⊥BC”与“AD平分∠ABC”的位置交换，得到的是否仍是真命题？
    ②若将题中“AD⊥BC”与“BD=CD”的位置交换，得到的是否仍是真命题？请你作出判断，在下列横线上填写“是”或“否”：①
    是
    是
     ②
    是
    是
     并对②的判断作出证明．（若是则写出证明过程；若不是则举出一个反例）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•山西）问题情境：将一副直角三角板（Rt△ABC和Rt△DEF）按图1所示的方式摆放，其中∠ACB=90°，CA=CB，∠FDE=90°，O是AB的中点，点D与点O重合，DF⊥AC于点M，DE⊥BC于点N，试判断线段OM与ON的数量关系，并说明理由．
    探究展示：小宇同学展示出如下正确的解法：
    解：OM=ON，证明如下：
    连接CO，则CO是AB边上中线，
    ∵CA=CB，∴CO是∠ACB的角平分线．（依据1）
    ∵OM⊥AC，ON⊥BC，∴OM=ON．（依据2）
    反思交流：
    （1）上述证明过程中的“依据1”和“依据2”分别是指：
    依据1：
    等腰三角形的三线合一（等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合）
    等腰三角形的三线合一（等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合）

    依据2：
    角平分线上的点到角的两边的距离相等
    角平分线上的点到角的两边的距离相等

    （2）你有与小宇不同的思考方法吗？请写出你的证明过程．
    拓展延伸：
    （3）将图1中的Rt△DEF沿着射线BA的方向平移至如图2所示的位置，使点D落在BA的延长线上，FD的延长线与CA的延长线垂直相交于点M，BC的延长线与DE垂直相交于点N，连接OM、ON，试判断线段OM、ON的数量关系与位置关系，并写出证明过程．

    查看答案和解析>>

    科目：初中数学 来源：同步练习数学　　九年级上册 题型：008

    判断对错

    三角形的一条中线把三角形分成的两个小三角形全等．

    (　　)

    查看答案和解析>>

    同步练习册答案