
如图所示,海关缉私巡逻艇在东海海域执行巡逻任务时,发现在其所处位置O点的正北方向10海里的A点有一涉嫌走私船只,正以24海里/时的速度向正东方向航行,为迅速实施检查,巡逻艇调整好航向,以26海里/时的速度追赶,在涉嫌船只不改变航向和航速的前提下,巡逻艇沿什么方向需几小时才能最快追上涉嫌船只?

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
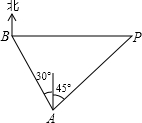 一海上巡逻艇在A处巡逻,突然接到上级命令,在北偏西30°方向且距离A处20海里的B港口,有一艘走私艇沿着正东方向以每小时50海里的速度驶向公海,务必进行拦截,巡逻艇马上沿北偏东45°的方向快速追击,恰好在临近公海的私快艇拦截住,如图所示,试求巡逻艇的速度.(结果取整数,参考数据:
一海上巡逻艇在A处巡逻,突然接到上级命令,在北偏西30°方向且距离A处20海里的B港口,有一艘走私艇沿着正东方向以每小时50海里的速度驶向公海,务必进行拦截,巡逻艇马上沿北偏东45°的方向快速追击,恰好在临近公海的私快艇拦截住,如图所示,试求巡逻艇的速度.(结果取整数,参考数据:| 2 |
| 3 |
| 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 发时,在其前方20千米处有一游轮以每小时20千米的速度匀速驶向终点B码头.
发时,在其前方20千米处有一游轮以每小时20千米的速度匀速驶向终点B码头.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 发时,在其前方20千米处有一游轮以每小时20千米的速度匀速驶向终点B码头.
发时,在其前方20千米处有一游轮以每小时20千米的速度匀速驶向终点B码头.查看答案和解析>>
科目:初中数学 来源:2011年湖北省鄂州市鄂城区订祖镇中考数学模拟试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com