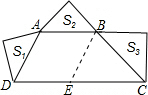
解:(1)作BE∥AD于E,则四边形ABED是平行四边形.
∴∠BEC=∠ADC,DE=AB=2010.
又∠ADC+∠BCD=90°,
∴∠EBC=90°.
∵S
1+S
3=4S
2,S
2=

×

×2010×2010,
∴BE
2+BC
2=4(S
1+S
3)=2010×2010×4,
∴CE=4020.
∴CD=6030.
(2)(15,15)、(60、60)、(15,60)、(60,15)、(240,240)、(135,540)、(540,135).
分析:(1)作BE∥AD于E,则四边形ABED是平行四边形,得∠BEC=∠ADC,DE=AB=2010,则∠EBC=90°.要求CD的长,只需根据勾股定理求得CE的长.结合等腰直角三角形的面积公式和S
1+S
3=4S
2,即可求解;
(2)根据题意,只需保证
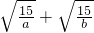
=2或

或

即可.
点评:(1)综合运用了平行四边形的判定及性质、勾股定理以及等腰直角三角形的性质.
注意:根据等腰直角三角形斜边上的高也是斜边上的中线,斜边上的中线等于斜边的一半,知等腰直角三角形的面积等于斜边的平方的一半.
(2)考查了二次根式的化简.


 也是整数,请写出所有满足条件的有序数对(a,b).
也是整数,请写出所有满足条件的有序数对(a,b). 解:(1)作BE∥AD于E,则四边形ABED是平行四边形.
解:(1)作BE∥AD于E,则四边形ABED是平行四边形. ×
× ×2010×2010,
×2010×2010,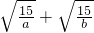 =2或
=2或 或
或 即可.
即可.

 初中暑期衔接系列答案
初中暑期衔接系列答案