Question

在三角形ABC中，AB=15，AC=41，AD⊥BC于D点，AD=9，求BC的值．

Answer 1

解：①如图所示：
∵AD⊥BC于D点，
∴△ADB和△ADC是直角三角形
∵在Rt△ADB中，AB=15，AD=9，
∴BD==12，
∴在Rt△ADC中，
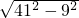
∴CD==40，
∴BC=BD+CD=12+40=52．
②如图所示：有①知BD=12，CD=40，
∴BC=CD-BD=40-12=28；
∴BC=52或28．
分析：根据勾股定理可分别求得BD与CD的长，从而不难求得BC的长．
点评：此题主要考查学生对勾股定理的运用能力．