
分析 根据新运算和完全平方公式、平方差公式可以化简题目中所求的式子.
解答 解:∵a*b=a2+ab+b2,
∴(x+$\frac{1}{2}$)*(x-$\frac{1}{2}$)
=$(x+\frac{1}{2})^{2}+(x+\frac{1}{2})(x-\frac{1}{2})+(x-\frac{1}{2})^{2}$
=${x}^{2}+x+\frac{1}{4}+{x}^{2}-\frac{1}{4}+{x}^{2}-x+\frac{1}{4}$
=3${x}^{2}+\frac{1}{4}$.
点评 本替考查整式的混合运算、新运算,解题的关键是明确新运算的应用和整式的混合运算的计算方法.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
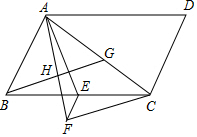 在平行四边形ABCD中,AC是对角线,∠ACD=90°.点E是BC的中点,AF平分∠BAC,CF⊥AF于点F.连接EF.
在平行四边形ABCD中,AC是对角线,∠ACD=90°.点E是BC的中点,AF平分∠BAC,CF⊥AF于点F.连接EF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
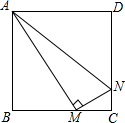 如图,正方形ABCD的边长为1cm,M、N分别是BC、CD上两个动点,且始终保持AM⊥MN,则△ADN的最小面积为$\frac{3}{8}$cm2.
如图,正方形ABCD的边长为1cm,M、N分别是BC、CD上两个动点,且始终保持AM⊥MN,则△ADN的最小面积为$\frac{3}{8}$cm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com