(1)证明:∵∠OMC=∠ONQ=90°,
∵∠MOP=90°-∠PON,∠NOQ=90°-∠PON
∴∠MOP=∠NOQ
∴△OMP∽△ONQ;
(2)解:AO=

=2,
OM=AOsin60°=

,
∴P纵坐标是-

,
P(x,-

),PM=|x|,
∵O是AB中点,
∴△BON≌△OAM,
∴AM=ON,
AM=AOcos60°=1,
由上面相似得

=
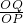
=

,
∴OP=

OQ,
OP
2=OM
2+MP
2=3+x
2
OQ
2=

=

,
L
2=

,
L=

,
CM=ON=AM=1
∴A(-1,-

),C(1,-

),
∴-1≤x≤1,
(3)解:PQ=L=

,
AC=2,
则CM=1,
∴CP=1-x,
∵
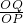
=

,
∴

=

,
PM=|x|,QN=

ON=

,
CN=OM=

,
∴CQ=QN+CN=

+

,
∴S=

CQ•CP=

(

+

)(1-x)=

,
x
1=0,x
2=1-

,
∵-1<x<1,
∴x=1-

,
CP=1-x=1-(1-

)=

.
分析:(1)根据∠OMC=∠ONQ=90°,∠MOP=∠NOQ,即可得出△OMP∽△ONQ;
(2)根据OM=AOsin60°=

,求出P纵坐标,设P(x,-

),PM=|x|,根据△BON≌△OAM,得出AM=ON,AM=AOcos60°=1,由相似得

=
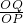
=

,OP=

OQ,得出OP
2和OQ
2,即可求出L
2,从而得出A和C点的坐标,最后求出L与x的函数关系式及定义域;
(3)根据PQ=L,得出CP=1-x和

,再根据PM=|x|,QN=

,得出CQ的值,最后根据S=

CQ•CP,得出x的值,即可求出CP的长;
点评:此题考查了相似三角形的判定与性质;解题的关键是根据相似三角形的性质求出线段的长度,在计算时要注意x的取值范围.

 时,试求CP的长.
时,试求CP的长.
 =2,
=2, ,
, ,
, ),PM=|x|,
),PM=|x|, =
=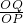 =
= ,
, OQ,
OQ, =
= ,
, ,
, ,
, ),C(1,-
),C(1,- ),
), ,
,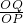 =
= ,
, =
= ,
, ON=
ON= ,
, ,
, +
+ ,
, CQ•CP=
CQ•CP= (
( +
+ )(1-x)=
)(1-x)= ,
, ,
, ,
, )=
)= .
. ,求出P纵坐标,设P(x,-
,求出P纵坐标,设P(x,- ),PM=|x|,根据△BON≌△OAM,得出AM=ON,AM=AOcos60°=1,由相似得
),PM=|x|,根据△BON≌△OAM,得出AM=ON,AM=AOcos60°=1,由相似得 =
=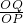 =
= ,OP=
,OP= OQ,得出OP2和OQ2,即可求出L2,从而得出A和C点的坐标,最后求出L与x的函数关系式及定义域;
OQ,得出OP2和OQ2,即可求出L2,从而得出A和C点的坐标,最后求出L与x的函数关系式及定义域; ,再根据PM=|x|,QN=
,再根据PM=|x|,QN= ,得出CQ的值,最后根据S=
,得出CQ的值,最后根据S= CQ•CP,得出x的值,即可求出CP的长;
CQ•CP,得出x的值,即可求出CP的长;

 考前必练系列答案
考前必练系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为