
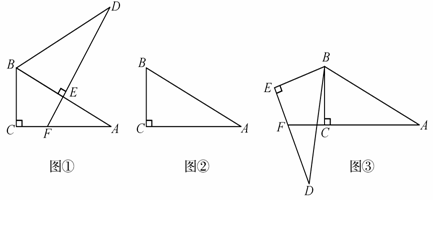
将两个全等的直角三角形ABC和DBE按图①方式摆放,其中∠ACB=∠DEB =90°,∠A=∠D =30°,点E落在AB上,DE所在直线交AC所在直线于点F.
(1)求证: AF+EF=DE;
(2)若将图①中的![]() 绕点B按顺时针方向旋转角
绕点B按顺时针方向旋转角![]() ,且
,且![]() ,其它条件不变,请在图②中画出变换后的图形,并直接写出你在⑴中猜想的结论是否仍然成立;
,其它条件不变,请在图②中画出变换后的图形,并直接写出你在⑴中猜想的结论是否仍然成立;
(3)若将图①中的![]() 绕点B按顺时针方向旋转角
绕点B按顺时针方向旋转角![]() ,且
,且![]() ,其它条件不变,如图③.你认为⑴中猜想的结论还成立吗?若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由.
,其它条件不变,如图③.你认为⑴中猜想的结论还成立吗?若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由.
 |
证明:
(1) 连接BF ∵△ABC≌△DBE, ∴BC=BE, AC=DE
∵∠ACB=∠DEB=90°
∴∠BCF=∠BEF=90°, ∵BF=BF
∴Rt△BFC≌Rt△BFE ∴CF=EF
∵AF+CF=AC, ∴AF+EF=DE
(2)如图②。(1)中的结论还成立
(3)不成立。此时AF,EF与DE的关系是AF-EF=DE
理由:连接BF(如图③)
∵△ABC≌△DBE, ∴BC=BE, AC=DE
∵∠ACB=∠DEB=90°
∴∠BCF=∠BEF=90°, ∵BF=BF
∴Rt△BFC≌Rt△BFE ∴CF=EF
∵AF-CF=AC, ∴AF-EF=DE
∴(1)中正确的结论AF-EF=DE



 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
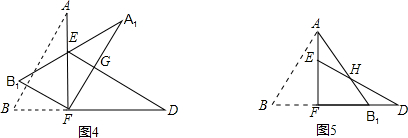
如图1,小明将一张矩形纸片沿对角线剪开,得到两张全等直角三角形纸片(如图2),量得他们的斜边长为10cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,使点B、F、D在同一条直线上,F为公共直角顶点.

小明在对这两张三角形纸片进行如下操作时遇到了两个问题,请你帮助解决。(1)将图3中的△ABF绕点F顺时针方向旋转30°到图4的位置,A1F交DE于点G,请你求出线段EG的长度;(2)将图3中的△ABF沿直线AF翻折到图5的位置,AB1交DE于点H,请证明:AH=DH.

查看答案和解析>>
科目:初中数学 来源: 题型:


查看答案和解析>>
科目:初中数学 来源:2011年广东省汕头市植英中学八年级第一学期期末考试试数学卷 题型:解答题
如图1,小明将一张矩形纸片沿对角线剪开,得到两张全等直角三角形纸片(如图2),量得他们的斜边长为10cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,使点B、F、D在同一条直线上,F为公共直角顶点.
小明在对这两张三角形纸片进行如下操作时遇到了两个问题,请你帮助解决。(1)将图3中的△ABF绕点F顺时针方向旋转30°到图4的位置,A1F交DE于点G,请你求出线段EG的长度;(2)将图3中的△ABF沿直线AF翻折到图5的位置,AB1交DE于点H,请证明:AH=DH.
查看答案和解析>>
科目:初中数学 来源:2011年广东省汕头市八年级第一学期期末考试试数学卷 题型:解答题
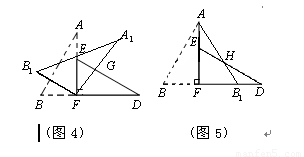
如图1,小明将一张矩形纸片沿对角线剪开,得到两张全等直角三角形纸片(如图2),量得他们的斜边长为10cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,使点B、F、D在同一条直线上,F为公共直角顶点.

小明在对这两张三角形纸片进行如下操作时遇到了两个问题,请你帮助解决。(1)将图3中的△ABF绕点F顺时针方向旋转30°到图4的位置,A1F交DE于点G,请你求出线段EG的长度;(2)将图3中的△ABF沿直线AF翻折到图5的位置,AB1交DE于点H,请证明:AH=DH.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com