
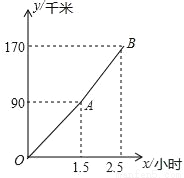
����һ�ڡ��ڼ䣬����ʦһ���Լ���ȥ�����170ǧ��ij�أ�������������ҵľ���y��ǧ�ף���������ʻʱ��x��Сʱ��֮��ĺ���ͼ��
��1�������dz�����Сʱʱ����Ҷ���ǧ�ף�
��2�����AB��ͼ��ĺ�������ʽ��
��3�����dz���2Сʱʱ����Ŀ�ĵػ��ж���ǧ�ף�

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��������2017-2018ѧ���һѧ�ڰ��꼶��ѧ�����Ծ� ���ͣ������
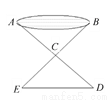
��ͼ����һ������Ҫ���������A��B����ľ��룬������ƽ����ȡһ������ֱ�ӵ���A��B�����C������AC���ӳ�AC����D��ʹCD=CA������BC���ӳ�BC����E��ʹCE=CB������DE����ô����________�ij��͵���AB�ij��� ������Ϊ�ɸ���________�����ж���ABC�ա�DEC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ĵ�ʡ���س���2016���^���꼶��ĩ���� ���ͣ������
��֪��AOB=90�㣬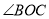 ����ǣ�ONƽ��
����ǣ�ONƽ��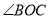 ��OMƽ�֡�AOB��
��OMƽ�֡�AOB��
��1����ͼ1��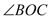 =30�㣬��
=30�㣬��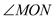 �Ķ�����
�Ķ�����
��2��������OC���ŵ�O�˶�����AOB���ڲ�����ͼ2�����ڣ�1������������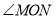 �Ķ�����
�Ķ�����
��3������AOB=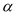 ��90���
��90���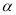 ��180�㣩��
��180�㣩��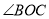 =
= 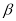 ��0�㣼
��0�㣼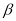 ��90�㣩�����ú���
��90�㣩�����ú���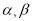 ��ʽ��ֱ�ӱ�ʾ�����������
��ʽ��ֱ�ӱ�ʾ�����������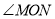 �Ķ�����
�Ķ�����
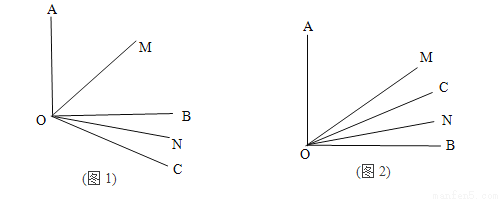
���𰸡���1��60�㣻��2��30�㣻��3���١�MON��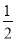 ��
��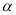 ��
��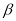 �������ڡ�MON��
�������ڡ�MON��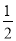 ��
��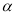 ��
��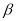 ����
����
�������������������1�����ڡ�AOB=90�㣬��BOC=30�㣬OMƽ�֡�AOB��ONƽ�֡�BOC�����Կ�����á�MOB�͡�NOB�Ķ�����������á�MON�Ķ�������2����ȣ�1���ķ�����⼴�ɣ���3����ϣ�1����2����ļ��㷽����⼴��.
���������
��1����OMƽ�֡�AOB��ONƽ�֡�BOC��
���BOM��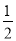 ��AOB����BON��
��AOB����BON��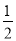 ��BOC��
��BOC��
�ߡ�AOB��90�㣬��BOC��30�㣬
���BOM��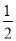 ��90�㣽45�㣬��BON��
��90�㣽45�㣬��BON��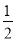 ��30�㣽15�㣬
��30�㣽15�㣬
���MON����BOM����BON��45�㣫15�㣽60�㣮
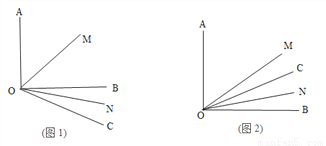
��2���ɣ�1����֪����BOM��45�㣬��BON��15�㣬
���MON����BOM����BON��45�㣭15�㣽30�㣮
��3���١�MON��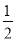 ��
��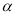 ��
��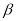 �����ڡ�MON��
�����ڡ�MON��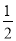 ��
��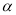 ��
��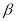 ����
����
�㾦��������Ҫ����ѧ����ƽ���ߵĶ��弰�ǵļ������������գ��ڽ�������֮��Ĺ�ϵʱ��Ҫ���������֪������ͼ�е���������.
�����͡������
��������
27
��1����֪�߶�AB=8cm�����߶�AB����һ��C����BC=4cm��MΪ�߶�AC���е㣮
�����߶�AM�ij���
������C���߶�AB���ӳ����ϣ�AM�ij������Ƕ����أ�
��2����ͼ��AD=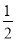 DB��E��BC���е㣬BE=
DB��E��BC���е㣬BE=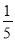 AC=2cm����DE�ij���
AC=2cm����DE�ij���
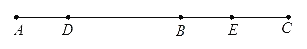
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ĵ�ʡ���س���2016���^���꼶��ĩ���� ���ͣ���ѡ��
��ͼ����֪��AOB=70�㣬OC�ǡ�AOB��ƽ���ߣ�OD�ǡ�BOC��ƽ���ߣ���ô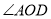 �Ķ����ǣ� ��
�Ķ����ǣ� ��
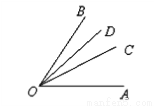
A. 52º B. 52º30�� C. 50º10�� D. 52º50��
B ���������ߡ�AOB=70�㣬OC�ǡ�AOB��ƽ���ߣ� ���AOC=��COB=��AOB=35�㣻 ��OD�ǡ�BOC��ƽ���ߣ� ���COD=��COB=17.5�㣻 ��=��AOC=��COD =35��+17.5��=52.5��= 52º30��. ��ѡB.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ĵ�ʡ���س���2016���^���꼶��ĩ���� ���ͣ���ѡ��
���в���ͬ������ǣ� ��
A. ��ab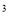 ��b
��b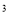 a B. 12��0 C. 2xyz�룭
a B. 12��0 C. 2xyz�룭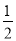 zyx D. 3x
zyx D. 3x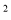 y�룭6xy
y�룭6xy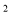
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ�²ᣨ�˽̰棩����ĩ�����(һ) ���ͣ������
��ͼ����?ABCD�У�AD��2AB����F��AD���е㣬��CE��AB������E���߶�AB�ϣ�����EF��CF�������н�����һ����������____��(��������ȷ���۵���Ŷ����ں�����)
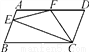
�١�DCF��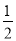 ��BCD����EF��CF����S��BEC��2S��CEF���ܡ�DFE��3��AEF.
��BCD����EF��CF����S��BEC��2S��CEF���ܡ�DFE��3��AEF.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ�²ᣨ�˽̰棩����ĩ�����(һ) ���ͣ������
�ں���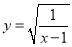 �У��Ա���x��ȡֵ��Χ��______��
�У��Ա���x��ȡֵ��Χ��______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶���ϣ���һ���¿���ѧ�Ծ� ���ͣ������
�����з��̣�
��1��x2��9=0 ��2��x2��3x��4=0
(1) x = �� 3 (2) x1=4 , x2= -1 ����������������� (1) ��С����Խ������������ƽ���ʽ������ʽ�ֽ⣬ͨ����ʽ�ֽⷨ�ⷽ�̣�Ҳ���Խ������������Ⱥ��Ҳ࣬����ֱ�ӿ�ƽ�����ⷽ��. (2) ��С���������ʮ����˷���������������ʽ�ֽ⣬ͨ����ʽ�ֽⷨ�ⷽ�̣�Ҳ��������һԪ���η��̵������ʽ�ⷽ��. ��������� (1) (����ʽ�ֽⷨΪ��...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶����Ԫ�µ�����ѧ�Ծ���2�� ���ͣ���ѡ��
�����ĸ�ͼ���У�������Գ�ͼ���������ĶԳ�ͼ�ε���( )
A. 
B. 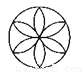
C. 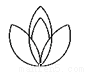
D. 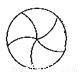
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com