练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

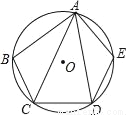
    如图，在⊙O的内接五边形ABCDE中，∠CAD=30°，则∠B+∠E=　 　．

    210°． 【解析】试题分析：连接CE，根据圆内接四边形对角互补可得∠B+∠AEC=180°，再根据同弧所对的圆周角相等可得∠CED=∠CAD=30°，然后求解得∠B+∠E=180°+30°=210°．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2016-2017学年河北省张家口市桥东区七年级（下）期末数学试卷 题型：单选题

    已知在△ABC中，∠A与∠C的度数比是5：7，且∠B比∠A大10°，那么∠B为（　　）

    A. 40° B. 50° C. 60° D. 70°

    C 【解析】依题意可设∠A与∠C的度数分别为5n°、7n°，则∠B=∠A+10°=5n°+10°， 在△ABC中，∠A+∠B+∠C=180°，即5n°+5n°+10°+7n°=180°，解得n°=10°． 所以∠B=60°．故选C．

    查看答案和解析>>

    科目：初中数学 来源：湖北省黄冈市2017-2018学年八年级（上）期中数学试 题型：解答题

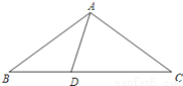
    如图，点D是△ABC的边BC上的一点，∠B=∠BAD=∠C，∠ADC=72°．试求∠DAC的度数．

    72° 【解析】试题分析：先根据三角形外角的性质得出∠ADC=∠B+∠BAD，再由∠B=∠BAD可知∠B=∠BAD=36°，在△ADC中，根据三角形内角和定理即可得出结论． 试题解析：∵∠ADC是△ABD的外角，∠ADC=72°， ∴∠ADC=∠B+∠BAD． 又∵∠B=∠BAD， ∴∠B=∠BAD=36°． ∵∠B=∠BAD=∠C， ∴∠C=36°． ...

    查看答案和解析>>

    科目：初中数学 来源：湖北省黄冈市2017-2018学年八年级（上）期中数学试 题型：单选题

    在八边形内任取一点，把这个点与八边形各顶点分别连接可得到几个三角形（　　）

    A. 5个 B. 6个 C. 7个 D. 8个

    D 【解析】如图 ，或者根据八边形内一点，和任意一边的两端点均可构成三角形，所以可求得三角形的个数为8. 故选：D．

    查看答案和解析>>

    科目：初中数学 来源：广东省汕头市潮南区两英镇2018届九年级上学期期末质检数学试卷 题型：解答题

    已知抛物线y=ax2+bx﹣8（a≠0）的对称轴是直线x=1，

    （1）求证：2a+b=0；

    （2）若关于x的方程ax2+bx﹣8=0，有一个根为4，求方程的另一个根．

    （1）见解析；（2）-2 【解析】试题分析：（1）根据抛物线的对称轴方程进行证明即可； （2）根据抛物线与x轴的交点问题可判断抛物线y=ax2+bx﹣8（a≠0）与x轴的一个交点坐标为（4，0），然后利用抛物线的对称性可得到抛物线y=ax2+bx﹣8（a≠0）与x轴的另一个交点坐标为（﹣2，0），从而得到方程ax2+bx﹣8=0另一个根． 试题解析：【解析】 （1）∵抛物线的对...

    查看答案和解析>>

    科目：初中数学 来源：广东省汕头市潮南区两英镇2018届九年级上学期期末质检数学试卷 题型：填空题

    一元二次方程x（x+3）=0的解是_____________________．

    x1=0，x2=﹣3 【解析】∵， ∴或， 解得： .

    查看答案和解析>>

    科目：初中数学 来源：广东省汕头市潮南区两英镇2018届九年级上学期期末质检数学试卷 题型：单选题

    如图，BD是⊙O的直径，点A、C在⊙O上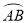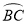，=，∠AOB=60°，则∠BDC的度数是（ ）.

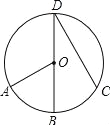
    A．60° B．45° C．35° D．30°

    D． 【解析】 试题分析：直接根据圆周角定理求解．连结OC，如图，∵=，∴∠BDC=∠BOC=∠AOB=×60°=30°． 故选：D．

    查看答案和解析>>

    科目：初中数学 来源：江苏省2017-2018学年七年级上学期第二次月考数学试卷 题型：填空题

    一项工程，甲独做a天完成；乙独做b天完成，则甲乙合做________天完成.

    【解析】根据题意，把总工作量看作“1”，可知甲的工作效率为，乙的工作效率为，则甲乙合做需要1÷（+）=. 故答案为： .

    查看答案和解析>>

    科目：初中数学 来源：辽宁省大连市沙河口区孙家沟九年制学校2018届九年级（上）期中数学试卷 题型：解答题

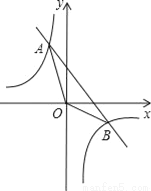
    如图所示，一次函数y=kx+b的图象与反比例函数y=﹣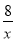的图象交于A、B两点，且点A的横坐标和点B的纵坐标都是﹣2，

    （1）求一次函数的解析式；

    （2）求△AOB的面积．

    （3）直接写出kx+b+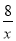＞0的解集．

    （1）y=﹣x+2；（2）6；（3）由函数图象可得当x＜﹣2或0＜x＜4时，kx+b+＞0． 【解析】试题分析：（1）先求出A，B两点坐标，将其代入一次函数关系式即可； （2）根据一次函数与y轴的交点为（0，2），则△AOC和△BOC的底边长为2，两三角形的高分别为|x1|和|x2|，从而可求得其面积； （3）由函数图象得出直线在双曲线上方时x的取值范围． 试题解析：（1）...

    查看答案和解析>>

    同步练习册答案