
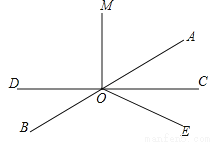
如图,已知直线AB与CD交于点O,OM⊥CD,OA平分∠MOE,且∠BOD=28°,求∠AOM,∠COE的度数.
科目:初中数学 来源:江苏省宿迁市2017-2018学年上学期第二次形成性测试七年级数学试卷 题型:填空题
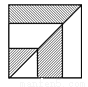
如图所示的正方形边长为4,则图中阴影部分的面积是____.
查看答案和解析>>
科目:初中数学 来源:上海市青浦区2018届九年级上学期期末调研测试数学试卷 题型:单选题
如果一次函数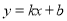 的图像经过一、二、三象限,那么
的图像经过一、二、三象限,那么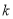 、
、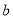 应满足的条件是( )
应满足的条件是( )
A. 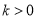 ,且
,且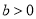 B.
B. 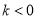 ,且
,且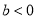 C.
C. 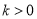 ,且
,且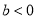 D.
D. 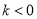 ,且
,且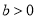
查看答案和解析>>
科目:初中数学 来源:浙江省余姚市2017-2018学年七年级上学期期中考试数学试卷 题型:单选题
将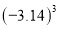 ,
, 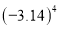 ,
, 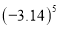 从小到大排列正确的是( )
从小到大排列正确的是( )
A. 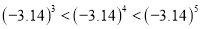 B.
B. 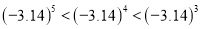
C. 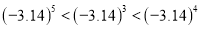 D.
D. 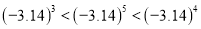
查看答案和解析>>
科目:初中数学 来源:浙江省余姚市2017-2018学年七年级上学期期中考试数学试卷 题型:单选题
今年余姚市上半年接待国内外游客650多万人次,实现旅游总收入61亿元,其中,61亿用科学计数法表示是( )
A. 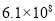 B.
B. 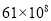 C.
C. 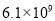 D.
D. 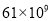
查看答案和解析>>
科目:初中数学 来源:海南省定安县2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
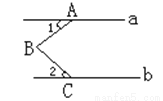
如图,直线a∥b,且∠1=28°,∠2=50°,则∠ABC=_______.
查看答案和解析>>
科目:初中数学 来源:海南省定安县2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
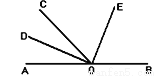
如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°,则∠COE=( )
A. 80° B. 75° C. 70° D. 65°
D 【解析】【解析】 ∵OD平分∠AOC,∠AOC=50°,∴∠COD=∠AOD=∠AOC=×50°=25°,∴∠COE=∠DOE﹣∠COD=90°﹣25°=65°.故选D.查看答案和解析>>
科目:初中数学 来源:云南省2018届九年级上学期期中考试数学试卷 题型:解答题
观察下列计算
15× 15=1 ×2 ×100+25
25× 25=2×3 ×100+25
35× 35=3×4×100+25 ………
写出一般的规律为_________,请运用所学知识证明你的结论.
(10n+5)(10n+5)=100n(n+1)+25 【解析】试题分析:根据数字变化规律得出个位是5的两个相同的数的乘积等于这个数的十位数字乘以十位数字加1再乘以100再加25,进而得出答案. 试题解析:∵左边=25(2n-1)2=25(4n2-4n+1)=100n2-100n+25, 右边=100n2-100n+25, ∴左边=右边, ∴5(2n-1)×5(2n-...查看答案和解析>>
科目:初中数学 来源:上海市长宁区2018届九年级上学期期末质量检测数学试卷 题型:解答题
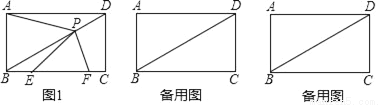
已知在矩形ABCD中,AB=2,AD=4.P是对角线BD上的一个动点(点P不与点B、D重合),过点P作PF⊥BD,交射线BC于点F.联结AP,画∠FPE=∠BAP,PE交BF于点E.设PD=x,EF=y.
(1)当点A、P、F在一条直线上时,求△ABF的面积;
(2)如图1,当点F在边BC上时,求y关于x的函数解析式,并写出函数定义域;
(3)联结PC,若∠FPC=∠BPE,请直接写出PD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com