练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    图形变化：

    Ⅰ．如图，分别以直角三角形的三边为直径向三角形外作三个半圆，你能找出这三个半圆的面积之间有什么关系吗？请说明理由．

    Ⅱ．如图，如果直角三角形两直角边的长分别为3和4，以直角三角形的三边

    为直径作半圆，你能利用上面中的结论求出阴影部分的面积吗？

    答案：
    解析：

    　　S1＋S2＝S3　3分

    　　S阴影＝6　6分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    已知：在Rt△ABC中，∠ABC=90°，D是AC的中点，⊙O经过A、D、B三点，CB的延长线交⊙O于点E（如图1）．
    在满足上述条件的情况下，当∠CAB的大小变化时，图形也随着改变（如图2），在这个变化过程中，有些线段总保持着相等的关系．
    （1）观察上述图形，连接图2中已标明字母的某两点，得到一条新线段精英家教网与线段CE相等，请说明理由；
    （2）在图2中，过点E作⊙O的切线，交AC的延长线于点F．
    ①若CF=CD，求sin∠CAB的值；
    ②若
    CFCD
    =n（n＞0），试用含n的代数式表示sin∠CAB（直接写出结果）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    25、阅读材料：
    如图（一），在已建立直角坐标系的方格纸中，图形①的顶点为A、B、C，要将它变换到图④（变换过程中图形的顶点必须在格点上，且不能超出方格纸的边界）．
    例如：将图形①作如下变换（如图二）．
    第一步：平移，使点C（6，6）移至点（4，3），得图②；
    第二步：旋转，绕着点（4，3）旋转180°，得图③；
    第三步：平移，使点（4，3）移至点O（0，0），得图④．
    则图形①被变换到了图④．

    解决问题：
    （1）在上述变化过程中A点的坐标依次为：
    （4，6）→（
    2
    ，
    3
    ）→（
    6
    ，
    3
    ）→（
    2
    ，
    0
    ）
    （2）如图（三），仿照例题格式，在直角坐标系的方格纸中将△DEF经过平移、旋转、翻折等变换得到△OPQ．（写出变换步骤，并画出相应的图形）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

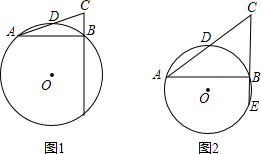
    已知：在Rt△ABC中，D为AC的中点，⊙O经过A、D、B三点，CB的延长线交⊙O于E（如图1）；在满足上述条件下，当∠CAB的大小变化时，图形也随着改变（如图2）；在这个变化过程中，有些总保持着相等关系．观察右边图形，连接图中已标明的两点，得到一条新线段，证明它与线段CE相等．

    查看答案和解析>>

    科目：初中数学 来源：2005年全国中考数学试题汇编《锐角三角函数》（05）（解析版） 题型：解答题

    （2005•北京）已知：在Rt△ABC中，∠ABC=90°，D是AC的中点，⊙O经过A、D、B三点，CB的延长线交⊙O于点E（如图1）．
    在满足上述条件的情况下，当∠CAB的大小变化时，图形也随着改变（如图2），在这个变化过程中，有些线段总保持着相等的关系．
    （1）观察上述图形，连接图2中已标明字母的某两点，得到一条新线段与线段CE相等，请说明理由；
    （2）在图2中，过点E作⊙O的切线，交AC的延长线于点F．
    ①若CF=CD，求sin∠CAB的值；
    ②若=n（n＞0），试用含n的代数式表示sin∠CAB（直接写出结果）．

    查看答案和解析>>

    科目：初中数学 来源：2009年江苏省苏州市黄桥镇横巷模拟考试数学试卷（解析版） 题型：解答题

    （2005•北京）已知：在Rt△ABC中，∠ABC=90°，D是AC的中点，⊙O经过A、D、B三点，CB的延长线交⊙O于点E（如图1）．
    在满足上述条件的情况下，当∠CAB的大小变化时，图形也随着改变（如图2），在这个变化过程中，有些线段总保持着相等的关系．
    （1）观察上述图形，连接图2中已标明字母的某两点，得到一条新线段与线段CE相等，请说明理由；
    （2）在图2中，过点E作⊙O的切线，交AC的延长线于点F．
    ①若CF=CD，求sin∠CAB的值；
    ②若=n（n＞0），试用含n的代数式表示sin∠CAB（直接写出结果）．

    查看答案和解析>>

    同步练习册答案