练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，已知函数y＝3x＋b和y＝ax－3的图象交于点P(－2，－5)，则根据图象可得不等式3x＋b＞ax－3的解集是( )

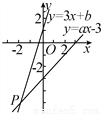
    A. x＜2 B. x＞2 C. x＞－2 D. x＜－2

    C 【解析】根据一次函数和不等式的关系，由函数的图像中的交点，可知符合条件的解集为：x＞-2. 故选：C.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版七年级下册 第一章 整式的乘除 1.6完全平方公式 同步测试 题型：单选题

    已知(a＋b)2=9，(a－b)2=5，则ab的值为( )

    A. －1 B. 1

    C. －4 D. 4

    B 【解析】试题解析：∵（a+b）2=9，（a-b）2=5， ∴a2+2ab+b2=9①，a2-2ab+b2=5②， ①-②得4ab=4， ∴ab=1. 故选A.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018河北省保定市莲池区七年级第一学期数学期末试卷 题型：单选题

    如图，O是直线AB上一点，OD平分∠BOC，∠COE=90°，若∠AOC=40°，则∠DOE为（　　）

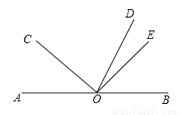
    A. 15° B. 20° C. 30° D. 45°

    B 【解析】∵O是直线AB上一点， ∴∠AOC+∠BOC=180°， ∵∠AOC=40°， ∴∠BOC=140°， ∵OD平分∠BOC， ∴∠COD=∠BOC=70°， ∵∠DOE=∠COE-∠COD，∠COE=90°， ∴∠DOE=20°. 故选B.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018 北师大版数学八年级下册 第二章 一元一次不等式和一元一次不等式组 单元检测卷 题型：解答题

    当x取什么值时，代数式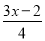－2x＋1的值为：(1)正数？(2)负数？(3)非负数？

    (1)x＜；(2)x＞； (3)x≤. 【解析】试题分析：根据题意，分别列出符合条件的不等式，然后解不等式即可求解. 试题解析：（1）由题意得－2x＋1＞0 解得x＜ （2）由题意得－2x＋1＜0 解得x＞ （3）由非负数可知： －2x＋1≥0 解得x≤

    查看答案和解析>>

    科目：初中数学 来源：2017-2018 北师大版数学八年级下册 第二章 一元一次不等式和一元一次不等式组 单元检测卷 题型：单选题

    一家电信公司给顾客提供两种上网收费方式：方式A以每分0.1元的价格按上网所用时间计算；方式B除收月基费20元外．再以每分0．05元的价格按上网所用时间计费。若上网所用时间为x分．计费为y元，如图．是在同一直角坐标系中．分别描述两种计费方式的函救的图象，有下列结论：

    ①图象甲描述的是方式A：

    ②图象乙描述的是方式B；

    ③当上网所用时间为500分时，选择方式B省钱．

    其中，正确结论的个数是

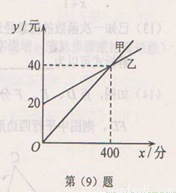
    A. 3 B. 2 C. 1 D. 0

    A 【解析】考查知识点：一次函数的应用；一次函数与一元一次不等式．

    查看答案和解析>>

    科目：初中数学 来源：北师大版八年级下册数学 第二章 一元一次不等式与一元一次不等式组 单元检测卷 题型：解答题

    已知方程ax+12=0的解是x=3，求满足关于y的不等式（a+2）y＜7的最小整数解．

    关于y的不等式（a+2）y＜7的最小整数解为﹣3． 【解析】试题分析：先将x=3代入ax+12=0，求出a的值，代入（a+2）y<7，再利用不等式的基本性质解不等式，然后从不等式的解集中找出适合条件的最小整数即可． 试题解析：将x=3代入ax+12=0， 得3a+12=0，解得a=﹣4． 把a=﹣4代入不等式，得﹣2y＜7， 解得y＞﹣3.5， 所以关于y的不等...

    查看答案和解析>>

    科目：初中数学 来源：北师大版八年级下册数学 第二章 一元一次不等式与一元一次不等式组 单元检测卷 题型：填空题

    不等式组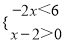的解集是________．

    x＞2 【解析】， 解不等式①得，x>?3， 解不等式②得，x>2， 所以，不等式组的解集是x>2. 故答案为：x>2.

    查看答案和解析>>

    科目：初中数学 来源：人教版初中数学七年级下册第八章《实际问题与二元一次方程组》同步练习 题型：解答题

    某文具店销售甲、乙两种圆规，当销售5只甲种、1只乙种圆规，可获利润25元，销售6只甲种、3只乙种圆规，可获利润39元．

    （1）问该文具店销售甲、乙两种圆规，每只的利润分别是多少元？

    （2）在（1）中，文具店共销售甲、乙两种圆规50只，其中甲种圆规为a只，求文具店所获得利润P与a的函数关系式，并求当a≥30时P的最大值．

    （1）甲种圆规每只的利润是4元，乙种圆规每只的利润是5元；（2）220． 【解析】试题分析：（1）设文具店销售甲、乙两种圆规，每只的利润分别是x元、y元，根据题意“销售5只甲种、1只乙种圆规，可获利润25元，销售6只甲种、3只乙种圆规，可获利润39元”，列出的方程组，解方程组即可；（2）根据题意可以列出文具店所获利p与a的函数关系式，然后根据当a≥30，可以求得p的最大值即可． 试题解...

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：期中达标检测卷 题型：解答题

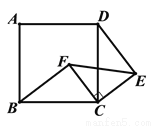
    如图，四边形ABCD是正方形，△ECF是等腰直角三角形，其中CE=CF， BC=5，CF=3，BF=4.

    求证：DE∥FC

    证明见解析. 【解析】试题分析：根据正方形以及△ECF的性质得出△BCF和△DCE全等，从而得出∠DEC=∠BFC，根据BC、CF和BF的长度得出∠BFC=90°，即∠DEC=90°，最后根据同旁内角互补两直线平行得出答案． 试题解析：∵四边形 ABCD是正方形 ∴∠BCF+∠FCD=90°，BC=CD， ∵△ECF是等腰直角三角形， ∴∠ECD+∠FCD=90°， CF=CE，...

    查看答案和解析>>

    同步练习册答案