练习册

  • 练习册
  • 试题
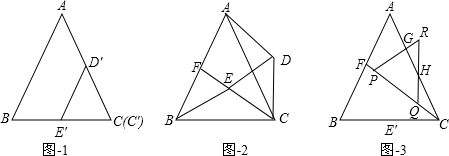    精英家教网 > 初中数学 > 题目详情

    写出函数y=3（x-1）2与y=x2-1所具有的一个共同性质________．

    开口向上
    分析：两函数解析式可看作抛物线解析式的顶点式，a＞0，开口向上，顶点坐标分别为（1，0），（0，-1），故对称轴，增减性，最大（小）值不同，与x轴（y轴）的交点也不同．
    解答：∵两个二次函数解析式中，二次项系数a=3和a=1，都为正数，
    ∴两抛物线都开口向上．
    点评：比较二次函数的性质，主要是比较抛物线的开口方向，顶点坐标，与x轴（y轴）的交点情况．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    图1是边长分别为4
    		3
    和3的两个等边三角形纸片ABC和C′D′E′叠放在一起（C与C′重合）．
    （1）操作：固定△ABC，将△C′D′E′绕点C顺时针旋转30°得到△CDE，连接AD，BE，CE的延长线交AB于F（图2）．
    探究：在图2中，线段BE与AD之间有怎样的大小关系？试证明你的结论；
    （2）操作：将图2中的△CDE，在线段CF上沿着CF方向以每秒1个单位的速度平移，平移后的△CDE设为△PQR（图3）．
    探究：设△PQR移动的时间为x秒，△PQR与△AFC重叠部分的面积为y精英家教网，求y与x之间的函数解析式，并写出函数自变量x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

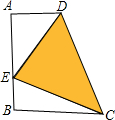    精英家教网如图，已知在梯形ABCD中，AD∥BC，∠A=90°，AD=2，AB=BC=4，在线段AB上有一动点E，设BE=x，△DEC的面积 S△DEC=y，问
    （1）你能找出y与x的函数关系吗？（若能写出函数关系式，就给出自变量x的取值范围）
    （2）S△DEC可能等于5吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，A、B两地相距30千米，甲骑自行车从A地出发前往B地，乙在甲出发1小时后骑摩托车从A地前往B地．
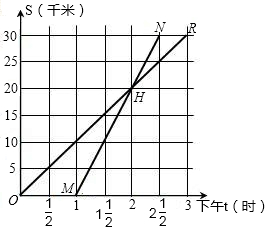
    精英家教网
    图中的线段OR和线段MN分别反映了甲和乙所行使的路程s（千米）与行驶时间t（小时）的函数关系．请根据图象所提供的信息回答问题：
    （1）乙骑摩托车的速度是每小时
     
    千米；
    （2）两人的相遇地点与B地之间的距离是
     
    千米；
    （3）甲所行驶的路程s（千米）与行驶时间t（小时）的函数关系式，并写出函数的定义域．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    精英家教网蓄电池的电压为定值，使用此电源时，电流I（A）与电阻（Ω）之间的函数关系图象如图所示，①通过图象你能得到什么信息（至少写出一条）？②写出函数关系式；③当电阻R=8Ω时，电流是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    图1是两个正方形纸片ABCD和CEFG叠放在一起，分别以BC边所在直线和BC边的中垂线为坐标轴建立如图所示的坐标系，其中B（-2，0），E（2，
    		2
    ），C（2，0），固定正方形ABCD，直线L经过AC两点；将正方形CEFG绕点C顺时针旋转135°得到正方形CE1F1G1，
    （1）在图2中求点E1的坐标，并直接写出点E1与直线L的位置关系．
    （2）利用（1）的结论，将图2中的正方形CE1F1G1在射线CA上沿着CA方向以每秒1个单位的速度平移，平移后的正方形CE1F1G1设为正方形PQRH（图3），当点R移动到点A停止，设正方形PQRH移动的时间为t秒，正方形PQRH与正方形ABCD重叠部分的面积为S，请直接写出S与t之间的函数解析式，并写出函数自变量t的取值范围．
    （3）在（2）的条件下，如果S=1时，过BP的直线为m，M点为直线m上的动点，N为直线L上的动点，那么是否存在平行四边形MNBC，如果存在，请求出M点的坐标，如果不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案