
 如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片
如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
分析 ①先判断出四边形CFHE是平行四边形,再根据翻折的性质可得CF=FH,然后根据邻边相等的平行四边形是菱形证明,判断出①正确;
②根据菱形的对角线平分一组对角线可得∠BCH=∠ECH,然后求出只有∠DCE=30°时EC平分∠DCH,判断出②错误;
③点H与点A重合时,设BF=x,表示出AF=FC=8-x,利用勾股定理列出方程求解得到BF的最小值,点G与点D重合时,CF=CD,求出BF=4,然后写出BF的取值范围,判断出③正确;
④过点F作FM⊥AD于M,求出ME,再利用勾股定理列式求解得到EF,判断出④正确.
解答 解:①∵FH与CG,EH与CF都是矩形ABCD的对边AD、BC的一部分,
∴FH∥CG,EH∥CF,
∴四边形CFHE是平行四边形,
由翻折的性质得,CF=FH,
∴四边形CFHE是菱形,
故①正确;
②∴∠BCH=∠ECH,
∴只有∠DCE=30°时EC平分∠DCH,
故②错误;
③点H与点A重合时,设BF=x,则AF=FC=8-x,
在Rt△ABF中,AB2+BF2=AF2,
即42+x2=(8-x)2,
解得x=3,
点G与点D重合时,CF=CD=4,
∴BF=4,
∴线段BF的取值范围为3≤BF≤4,
故③正确;
过点F作FM⊥AD于M,
则ME=(8-3)-3=2,
由勾股定理得,
EF=$\sqrt{M{F}^{2}+M{E}^{2}}$=2$\sqrt{5}$,
故④正确;
综上所述,结论正确的有①③④共3个;
故选:C.
点评 此题是四边形综合题,主要考查了折叠问题与菱形的判定与性质、勾股定理的综合应用,熟练掌握菱形的判定定理和性质定理、勾股定理是解本题的关键.


科目:初中数学 来源: 题型:解答题
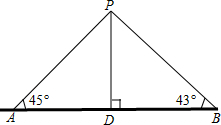 如图,某湖中有一个小岛,湖边有一条笔直的观光小道AB,现决定从小岛建一座与观光小道垂直的小桥PD,测得如下数据:AB=80.0m,∠PAB=45°,∠PBA=43°.求小桥PD的长.(结果精确到0.1m)
如图,某湖中有一个小岛,湖边有一条笔直的观光小道AB,现决定从小岛建一座与观光小道垂直的小桥PD,测得如下数据:AB=80.0m,∠PAB=45°,∠PBA=43°.求小桥PD的长.(结果精确到0.1m)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 由于发生山体滑坡灾害,武警救援队火速赶往灾区救援,探测出某建筑物废墟下方点C处有生命迹象.在废墟一侧地面上探测点A、B相距2米,探测线与该面的夹角分别是30°和45°(如图),试确定生命所在点C的深度(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果精确到0.1)
由于发生山体滑坡灾害,武警救援队火速赶往灾区救援,探测出某建筑物废墟下方点C处有生命迹象.在废墟一侧地面上探测点A、B相距2米,探测线与该面的夹角分别是30°和45°(如图),试确定生命所在点C的深度(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果精确到0.1)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com