
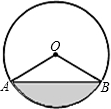
 如图,AB是⊙O的弦,OA=2,∠AOB=120°,则图中阴影部分的面积为________.(结果保留根号和π )
如图,AB是⊙O的弦,OA=2,∠AOB=120°,则图中阴影部分的面积为________.(结果保留根号和π ) -
- .
.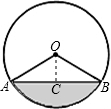 解:过O作OC⊥AB于C,如图,
解:过O作OC⊥AB于C,如图, (180°-120°)=30°,
(180°-120°)=30°, ,
, ,
, -
- •1•2
•1•2
 -
- .
. -
- .
. ;也考查了垂径定理和等腰三角形的性质以及含30度的直角三角形三边的关系.
;也考查了垂径定理和等腰三角形的性质以及含30度的直角三角形三边的关系. 

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com