练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    用配方法解一元二次方程2x2－6x＋1＝0时，此方程配方后可化为（ ）

    A. (x－)2 ＝ B. 2(x－)2 ＝ C. (x－)2 ＝ D. 2(x－)2 ＝

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：湖南省邵阳市2018年中考网上阅卷适应性考试数学试卷 题型：解答题

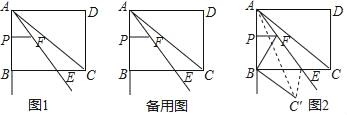
    如图1，矩形ABCD中，AB=4，AD=5，E为BC上一点，BE：CE=3：2，连接AE，点P从点A出发，沿射线AB的方向以每秒1个单位长度的速度匀速运动，过点P作PF∥BC交直线AE于点F．

    （1）线段AE=　 　；

    （2）设点P的运动时间为t（s），EF的长度为y，求y关于t的函数关系式，并写出t的取值范围；

    （3）当t为何值时，以F为圆心的⊙F恰好与直线AB、BC都相切？并求此时⊙F的半径；

    （4）如图2，将△AEC沿直线AE翻折，得到△AEC'，连结AC'，如果∠ABF=∠CBC′，求t值．（直接写出答案，不要求解答过程）．

    查看答案和解析>>

    科目：初中数学 来源：湖北省2018届九年级3月月考数学试卷 题型：单选题

    如图，为估算学校的旗杆的高度，身高米的小红同学沿着旗杆在地面的影子由向走去，当她走到点处时，她的影子的顶端正好与旗杆的影子的顶端重合，此时测得，，则旗杆的高度是（ ）

    A. 6.4m B. 7m C. 8m D. 9m

    查看答案和解析>>

    科目：初中数学 来源：吉林省2017～2018学年度第二学期期末学情分析样题 八年级数学试卷 题型：填空题

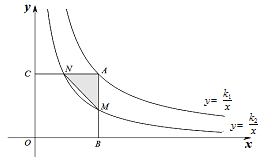
    反比例函数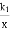y=、y=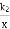在同一直角坐标系中的图象如图所示，则△AMN的面积为______．（用含有k1、k2的代数式表示）

    查看答案和解析>>

    科目：初中数学 来源：吉林省2017～2018学年度第二学期期末学情分析样题 八年级数学试卷 题型：填空题

    方程x2=2x的根是_________.

    查看答案和解析>>

    科目：初中数学 来源：江苏省无锡市惠山区2017-2018学年八年级下学期期末考试数学试卷 题型：解答题

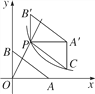
    如图，直线y＝k1x(x≥0)与双曲线y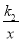＝ (x＞0)相交于点P(2，4)．已知点A(4，0)，B(0，3)，连接AB，将Rt△AOB沿OP方向平移，使点O移动到点P，得到△A′PB′.过点A′作A′C∥y轴交双曲线于点C，连接CP.

    (1)求k1与k2的值；

    (2)求直线PC的解析式；

    (3)直接写出线段AB扫过的面积．

    查看答案和解析>>

    科目：初中数学 来源：江苏省无锡市惠山区2017-2018学年八年级下学期期末考试数学试卷 题型：填空题

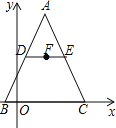
    如图，在△ABC中，AB=AC=13，DE是△ABC的中位线，F是DE的中点，已知B（-1,0），C（9,0），则点F的坐标为______________.

    查看答案和解析>>

    科目：初中数学 来源：吉林省长春市校2018届九年级下学期第一次模拟考试数学试卷 题型：解答题

    设抛物线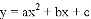与x轴的交点分别为A、B（点A在点B的左侧），顶点为C．若a、b、c满足，则称该抛物线为“正定抛物线”；若a、b、c满足，则称该抛物线为“负定抛物线”．特别地，若某抛物线既是“正定抛物线”又是“负定抛物线”，则称该抛物线为“对称抛物线”．

    （1）“正定抛物线”必经过x轴上的定点___________；“负定抛物线”必经过x轴上的定点___________．

    （2）若抛物线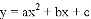是“对称抛物线”，且△ABC是等边三角形，求此抛物线对应的函数表达式．

    （3）若抛物线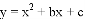是“正定抛物线”，设此抛物线交y轴于点D，△BCD的面积为S，求S与b之间的函数关系式．

    （4）设“正定抛物线”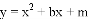(b>0)与x轴的交点分别为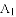、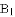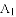（在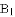的左侧），顶点为M；“负定抛物线”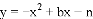(b>0)与x轴的交点分别为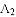、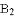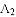（在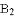的左侧），顶点为N．在两条抛物线所对应的函数表达式中，当同时满足y随x的增大而增大时的所有x的值在x轴上所对应的点恰好是线段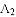 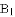（包括端点）时，直接写出此时以M、N、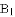、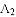为顶点的四边形的面积．

    查看答案和解析>>

    科目：初中数学 来源：广东省开平市2018届九年级上学期期末考试数学试卷 题型：填空题

    如图所示，在平行四边形ABCD中，E为CD上一点，连接AE，BD，且AE，BD交于点F，S△DEF：S△ABF=4：25，则DE：EC=（ ）

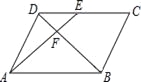
    A. 2：5 B. 2：3 C. 3：5 D. 3：2

    查看答案和解析>>

    同步练习册答案