
 如图,装潢公司利用一块三角形“边角余料”彩钢,按客户要求制作一块矩形台面、已知三角形彩钢的一边AB长1.8米,AB边上的高CD是0.9米.矩形的一边GH在边AB上,顶点E、F分别在AC、BC边上.若根据客户要求“制作后的矩形台面的长EF是宽EG的两倍,且面积不得少于0.4平方米”,请你帮助装潢公司计算一下这块三角形边角余料是否能制作出符合条件的矩形台面.(要求:写出计算过程)
如图,装潢公司利用一块三角形“边角余料”彩钢,按客户要求制作一块矩形台面、已知三角形彩钢的一边AB长1.8米,AB边上的高CD是0.9米.矩形的一边GH在边AB上,顶点E、F分别在AC、BC边上.若根据客户要求“制作后的矩形台面的长EF是宽EG的两倍,且面积不得少于0.4平方米”,请你帮助装潢公司计算一下这块三角形边角余料是否能制作出符合条件的矩形台面.(要求:写出计算过程)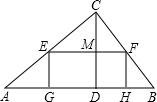 解:设△ABC的高CD与EF交于点M,
解:设△ABC的高CD与EF交于点M,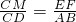 ,
,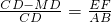 ,
,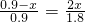 ,
,

科目:初中数学 来源:2009年上海市青浦区中考数学一模试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com