解:(1)证明:∵∠BAD=135°,且∠BAC=90°,
∴∠CAD=45°,即△ABC、△ADC都是等腰直角三角形;
∴AD=

AC,且∠D=∠ACB=45°;
又∵∠EAC=∠DAF=45°-∠FAC,
∴△AEC∽△AFD,
∴AE:AD=EC:FD=1:

,即EC=

FD;
∴BC=BE+

DF,即BE+

DF=AD.
(2)2BE+DF=AD;理由如下:

取BC的中点G,连接AG;
易知:∠DAC=∠BCA=30°,∠B=∠D=60°;
在Rt△ABC中,G是斜边BC的中点,则:
∠AGE=60°,AD=BC=2AG;
∵∠GAD=∠AGE=60°=∠EAF,
∴∠EAG=∠FAD=60°-∠GAF;
又∵∠AGE=∠D=60°,
∴△AGE∽△ADF,得:AG:AD=EG:FD=1:2;
即FD=2EG;
∴BC=2BG=2(BE+EG)=2BE+2EG=2BE+DF,即AD=2BE+DF.
(3)在Rt△ABC中,∠ACB=30°,AB=3,则BC=AD=6,EC=4.
①如图(2)①,过F作FH⊥BQ于H;

同(2)可知:DF=2EG=2,CF=CD-DF=1;
在Rt△CFH中,∠FCH=60°,则:
CH=

,FH=

;
易知:△ADF∽△QCF,由DF=2CF,可得CQ=

AD=3;
∴EQ=EC+CQ=4+3=7;
在R

t△EFH中,EH=EC+CH=

,FH=

;
由勾股定理可求得:EF=

.
②如图(2)②;
∵∠EAF=∠GAD=60°,
∴∠EAG=∠FAD=60°+∠FAG,
又∵∠EGA=∠D=60°,
∴△EAG∽△FAD,得:EG:FD=AG:AD=1:2;
即FD=2EG=10,FC=10-CD=7;
在Rt△FCN中,∠FCN=60°,
易求得FN=
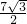
,NC=

,GN=

;
在等边△ABG中,AM⊥BG,易求得AM=

,MG=

,MN=MG-GN=1;
由于△AMQ∽△FNQ,得:AM:FN=MQ:NQ=3:7,即QN=

,MQ=

;
EQ=EB+BM+MQ=2+

+

=
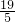
;
Rt△EFN中,EN=EG-NG=5-

=

,FN=
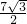
,
由勾股定理,得:EF=

;
综上可知:EQ=7或
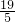
,EF=

或

.
分析:(1)此题要通过相似三角形求解;根据∠EAF=∠CAD=45°,可证得∠EAC=∠FAD,而∠ACB=∠D=45°,即可得△AEC∽△AFD,根据AC、AD的比例关系,即可得EC、FD的比例关系,由此得解.
(2)按照(1)的思路,此题要构造相似三角形来求解;取BC的中点G,连接AG;首先通过证△AGC∽△AFD来得到EG、FD的比例关系,然后根据BC=2(BE+EG)求得BE、CF、AD的等量关系式.
(3)此题应分两种情况:
①如(2),点E、F分别在线段BC、CD上;过F作FH⊥BQ于H,由(2)的相似三角形易得FD=2EG=2,那么CF=1,在Rt△CFH中,即可求出FH、CH的值;进而可由勾股定理求得EF的长;由相似三角形△ADF∽△QCF易得CQ的长,即可求出EQ的值;
②点E、Q分别在CB、DC的延长线上;分别过A、F作BC的垂线,设垂足为M、N;易求得AM、FN、BM、EN的长,进而可求出GM、MN的值,根据AM、FN的长,易求得△AMQ、FNQ的相似比,即可求出NQ、MQ的值,从而求得EQ、EF的长,由此得解.
点评:此题主要考查了平行四边形的性质、相似三角形的判定和性质以及勾股定理、直角三角形性质的综合应用,同时还涉及到分类讨论的数学思想,难度较大.

 DF=AD;
DF=AD;

 AC,且∠D=∠ACB=45°;
AC,且∠D=∠ACB=45°; ,即EC=
,即EC= FD;
FD; DF,即BE+
DF,即BE+ DF=AD.
DF=AD.

 ,FH=
,FH= ;
; AD=3;
AD=3; t△EFH中,EH=EC+CH=
t△EFH中,EH=EC+CH= ,FH=
,FH= ;
; .
.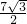 ,NC=
,NC= ,GN=
,GN= ;
; ,MG=
,MG= ,MN=MG-GN=1;
,MN=MG-GN=1; ,MQ=
,MQ= ;
; +
+ =
=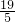 ;
; =
= ,FN=
,FN=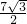 ,
, ;
;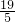 ,EF=
,EF= 或
或 .
.

 黄冈创优卷系列答案
黄冈创优卷系列答案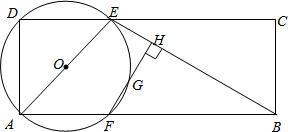 接AE、BE,以AE为直径作圆,交AB于点F,过点F作FH⊥BE于H,直线FH交⊙O于点G.
接AE、BE,以AE为直径作圆,交AB于点F,过点F作FH⊥BE于H,直线FH交⊙O于点G.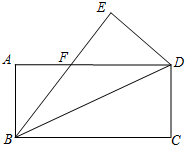 如图,已知矩形ABCD中,AB=4,BC=8,连接BD,将△BCD沿着BD翻折,C点落在E点处,BE交AD于F点.
如图,已知矩形ABCD中,AB=4,BC=8,连接BD,将△BCD沿着BD翻折,C点落在E点处,BE交AD于F点. 如图,已知正方形ABCD中,对角线AC、BD交于O点,过O点作OE⊥OF分别交DC于E,交BC于F,∠FEC的角平分线EP交直线AC于P
如图,已知正方形ABCD中,对角线AC、BD交于O点,过O点作OE⊥OF分别交DC于E,交BC于F,∠FEC的角平分线EP交直线AC于P