练习册

  • 练习册
  • 试题
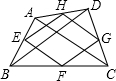    精英家教网 > 初中数学 > 题目详情

    四边形ABCD与四边形A1B1C1D1相似，相似比为2：3，四边形A1B1C1D1与四边形A2B2C2D2相似，相似比为5：4，则四边形ABCD与四边形A2B2C2D2相似且相似比为


    1. A.
      5：6
    2. B.
      6：5
    3. C.
      5：6或6：5
    4. D.
      8：15
    A
    分析：首先将2：3转化为10：15，将5：4转化为15：12，然后求得四边形ABCD与四边形A2B2C2D2相似比即可．
    解答：∵四边形ABCD与四边形A1B1C1D1相似，相似比为2：3，
    即：相似比为：10：15；
    四边形A1B1C1D1与四边形A2B2C2D2相似，相似比为5：4，即：15：12；
    ∴四边形ABCD与四边形A2B2C2D2且相似比为10：12，
    也就是 5：6．
    故选A．
    点评：本题考查了相似多边形的性质，解题的关键是将相似比进行转换．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网如图，已知凸四边形ABCD的两对角线BD与AC之比为k，菱形EFGH各顶点位于四边形ABCD的顺次四边之上，且EF∥AC，FG∥BD，则四边形ABCD与菱形EFGH的面积之比为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

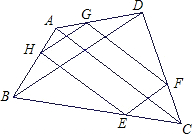    精英家教网在四边形ABCD中，AC、BD是四边形ABCD的两条对角线，点E、F、G、H分别是在四边形ABCD的四边上的动点，但E、F、G、H不与A、B、C、D重合，且EF∥BD∥GH，FG∥AC∥HE．
    （1）若对角线AC=BD=a（定值），求证：四边形EFGH的周长是定值；
    （2）若AC=m，BD=n，m、n为定值，但m≠n，则四边形EFGH的周长是定值吗？请指出，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

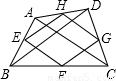
    11、如图，延长四边形ABCD的四边分别至E、F、G、H，使AB=nBE，BC=nCF，CD=nDG，DA=nAH（n＞0），则四边形EFGH与四边形ABCD的面积之比为
    （n2+2n+2）：n2
    （用含n的代数式表示）．

    查看答案和解析>>

    科目：初中数学 来源：2011年四川省南充市高坪中学九年级数学竞赛试卷（解析版） 题型：填空题

    如图，已知凸四边形ABCD的两对角线BD与AC之比为k，菱形EFGH各顶点位于四边形ABCD的顺次四边之上，且EF∥AC，FG∥BD，则四边形ABCD与菱形EFGH的面积之比为    ．

    查看答案和解析>>

    科目：初中数学 来源：2008年12月浙江省宁波市余姚市世南中学九年级数学竞赛试卷（解析版） 题型：解答题

    如图，延长四边形ABCD的四边分别至E、F、G、H，使AB=nBE，BC=nCF，CD=nDG，DA=nAH（n＞0），则四边形EFGH与四边形ABCD的面积之比为______（用含n的代数式表示）．

    查看答案和解析>>

    同步练习册答案